本标准包括统计学中常用的正态分布的三种数值表。 GB 4086.1-1983 统计分布数值表 正态分布 GB4086.1-1983 标准下载解压密码：www.bzxz.net
本标准包括统计学中常用的正态分布的三种数值表。

中华人民共和国国家标准
统计分布数值表
正态分布
Tables for statistical distributionsNormal distribution
UDC 311.13(083.5)
GB 4086.1--83
本标准包括统计学中常用的正态分布的三种数值表，它们的名称、表距和精度如下：正态分布密度函数表
正态分布函涵数表
正态分布分位数表
u=0 (0.01)4.99
u=0 (0.01)4.99
p=0.5(0.001)0.999
6位小数
6位小数
6位小数
本标准所指的正态分布是标准正态分布。表中的分位数对应于下侧概率。虽然表中给出6位小数，但是在使用中需要取几位，要由实际问题决定。在应用中不能满足要求时，可参考附录的处理方法。国家标准局1983-1221发布
1984~1001实施
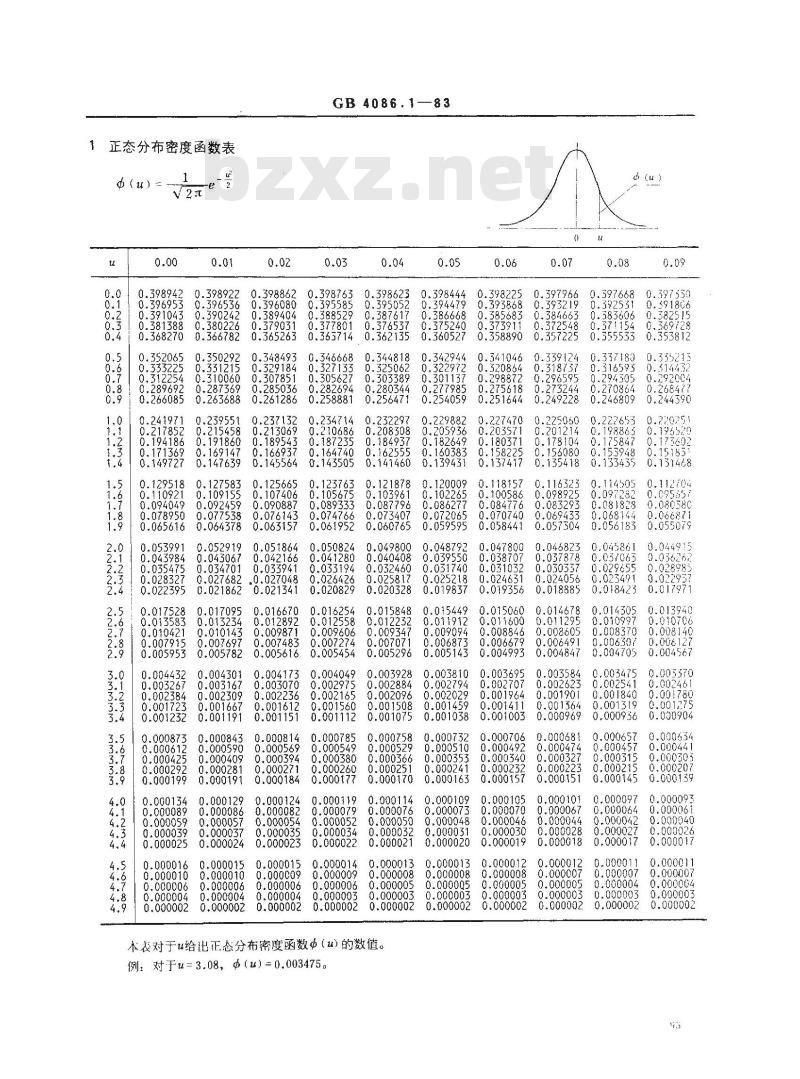
正态分布密度函数表
133383
381388
352069
194186
110921
1398922
390242
310060
287369
191860
0147639
0,000191
.000015
398862
285034
189543
145564
125665
107406
0+063157
000271
000015
GB 4086.1—83
398763
346668
282694
258881
234714
143505
123763
089333
026426
002165
.000079
000014
398623
344818
232297
162555
121878
103961
.009347
.000076
8:000005
本表对于u给出正态分布密度函数中（u）的数值。例：对于u=3.08，中（u）=0.003475。0.05
398444
342944
120009
.059595
.031740
上要变
203571
118157
084776
.000070
.000005
397966
393219
318737
178104
1001364
000681
397668
270864
198863
114505
068144
.014305
006307
397330
369728
31443:
292004
268477
196520
173602
151853
884930
.977250
995339
996533
997445
999032
999767
999892
999928
999987
999991
.999998
000000
791030
886861
986447
989556
998193
999065
999896
999980
999987
.999999
587064
793892
922196
996736
997599
999933
9Q9971
999988
999992
999997
999998
1590954
629300
966375
8:990099
999381
999566
999792
999858
999936
999982
999988
594835
770350
925066
959070
994457
Q:996928
999155
1999938
999983
.999989
8:999998
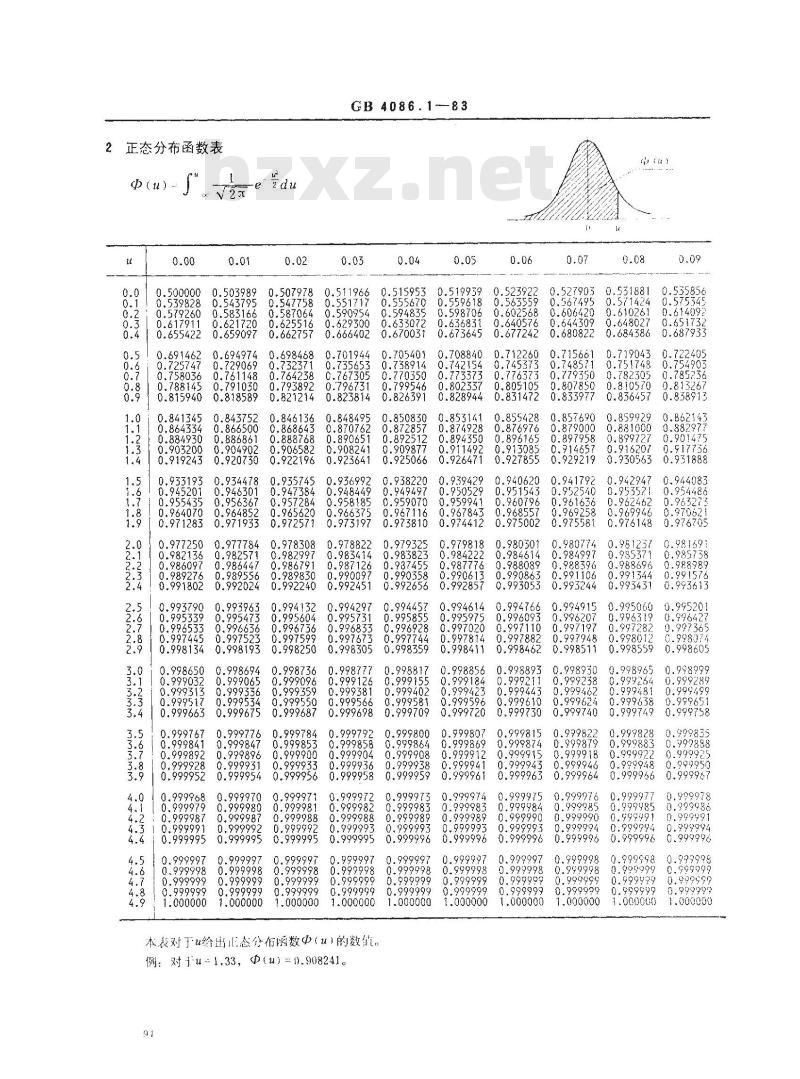
本表对了u给正态分布丽数中（u的数值。例：对u-1.33，Φ（u）=0.908241。91
598706
911492
939429
950529
967843
994614
.995975
997020
.999596
.999720
.999807
745373
.876976
.940620
980301
984614
988089
090863
994764
999211
299443
999961
999999
.644309
8:991166
751748
899727
930563
942947
：999481
.754903
917754
981691
985758
0:996427
997365
998074
999758
0.3999986
正态分布分位数表
100434
279319
1305481
358459
385320
524401
674490
706303
738847
994458
136431
.405072
475791
.644854
750686
\2du-p
027576
230118
255936
281926
334503
0 361133
0498687
527279
556308
585815
677640
742144
.919183
040732
131131
231864
762410
055174
156042
258527
.530161
712751
745450
135896
GB 4086.1--83
082813
158580
339809
562170
926859
.29883
1359463
1-425544
674665
035100
110516
.263714
535940
565108
365808
589268
2:144411
512144
本装对了下侧概率p给出止态分布的分位数up。例：对于p0.95，up=1.644854。p1.5时，up-
。例：
与双侧概率α相应的分位数为u
0. 510073
755415
11439531
170090
1.281552。
Q:428895
0512930
.541737
725737
938476
.378659
1446632
706043
825007
197286
092879
271508
404289
530068
995393
对 -α= 0.05, u1 -4 2 = uu.375 - 1.959964例：
Q:57691
765456
.870550
461056
538199
625763
.727934
852180
.097915
199336
250760
.276714
329206
355787
.382622
.409735
:493018
0:579873
.703089
735558
768820
838055
874217
911561
990356
.07583
170002
.398377
.546433
635234
739198
866296
GB4086.1—83
附录A
计算方法
（参考件）
这给出本标准三种数值表的计算方法。在本标准所列数表不能满足要求时，可参号这些算法及附录B的程序进行计算，或者使用插值方法作粗略计算。A.1定义与记号
本标准所指的止态分布是标准正态分布，其密度函数是b（u）
分布函数是
Φ(u）=
写下侧概率p对应的分位数up满足如下方程：1
A.2计算方法
(u)du。
du=p，
(up)-=0。
A.2.1正态分布密度函数的计算
真接按定义计算。
A，2.2正态分布函数的计算
用连分式遥近：
当03时有
当u3时有
r1-G（u)，当u≥0,
G(uj),
当uo。
式的精度取决于实际计算时连分式的项数。A.2.3正态分布分位数的计算
GB4086.1—83
使用A.3的选代方法计算，初始值由下式给出：up= sign(p-
y(2.0611786
y=-ln[4p(1-p)]。
上式的相对误差小于4.9×10-4。A.3分位数的选代计算
5.7262204
y+11.640595),
首先，寻找一个分位数的近似公式，并据此算出与下侧概率p对应的分位数。作为初始值。其次，根据分位数所满足的方程，使用基于二阶台劳（Taylor）展开的迭代求根法算出精度较高的分位数。过程如下：
为方便，把分位数所满足的方程记为F(r)=0,
r=ro +。
在附近对F（α)作二阶台劳展开0=F(α) =F(αa+△)
F(co) + F(xo)A+ F\(o)-
解之得
或等价地有
-F(xo)±V(F(x0))?-2F(ro)F\(ao)F\(co)
2F(ro)
F(xo)FV(F(2o))?-2F(xo)F\(ro) 由问题的意义，4只应取实根。因此当根号内取负值时，改令F(αo)
或等价地
F\(ro），
-2F(αo)
F(αo)
此外，根号的正负号选择应保证△|较小。亦即当F（α）>0时，式中分子的根号取正（或分母根号取负)；当F（α)<0时，4式中分子的根号取负（或分母根号取正）。求出4后，用+代替原来的o，重复上述过程，直至「△1小于允许误差。97
B.1说明
GB 4086.1--83
附录B
计算程序
（参考件）
这里给出用于本标准实际计算的两个FORTRAN语言了程序。它们是NORFD：用于计算正态分布的分布函数，NORXD：用于计算正态分布的分位数。程序使用的计算方法见附录A，
虽然本标准印出的数表只取6位小数，但程序的计算精度通常可达10~10程序
SUBROUTINE NORFD(U.P)
DOUBLE PRECISION U,P
** PURPOSE **
DISTRIBUTION FUNCTION OF NORMAL DISTRIBUTION** ARGUMENTS **
ON ENTRY
NORMAL DEVIATE
ON RETURN
LOWER PROBABILITY
** REQUIRED ROUTINES **
** ALGORITHM **
FOR NEGATIVE U
P(U) = PP(ABS(U)),
FOR NON-NEGATIVE U
P(U) = 1 - PP(U),
FOR U.GT.3
PP(U) = EXP(-U**2/2)/SQRT(2*PAI)*(1/U.+.1/U,+.2/U.+.+.k/U.+..+.).
NORF0001
NORF0002
NORF0003
NORF0004
NORFO005
NORF0006
NORF0007
NORF0008
NGRF0009
NORFO010
NORF0011
NORFO012
NORF0013
NORF0014
NORF0015
NORF0016
NORF0017
NORF0018
NORF0019
NORF0020
NORF0021
NORF0022
NDRF0023
NORF0024
(1) NORFO025
FOR U.GE.0 AND U.LE.3
PP(U)= 0.5 - EXP(-U**2/2)/SQRT(2*PAI)*(U/1.-.U**2/3.+。2*U**2/5..3*U**2/7.+.*.).
WHERE.+. AND.-. DENOTE CONTINUED FRACTIONINTEGER K
DOUBLE PRECISION Y.Y2,Z.FJ,S,BDATA K/28/S/~1.0D0/，B/3.000/Y = BABS(U)
Y2 = Y*Y
Z DEXP(-0.5D0*Y2)*0.39894228040143267800P = 0.0DO
IF(Y.LE.B)GO TO 20
NORF0026
NORF0027
(2) NORF0028
NORF0029
NORF0030
NORFO031
NORF0032
NORF0033
NORFO034
NORF0035
NORF0036
NORF0037
NORF0038
NORFC039
NORFO040
NORF0041
NORF0042
GB4086.1-83
FORMULA (1) IS EMPLOYEO FOR LARGE UDO 10 I=1.K
P = FJ/(Y + P)
FJ = FJ - 1.0D0
CONTINUE
P = Z/(Y
GO TO 40
20 CONTINUE
FORMULA (2) IS EMPLOYEO FOR SMALL U00 30 1 = 1.K
P = FJ*Y2/(2.0DO*FJ + 1.0D0 + S*P)s=s
FJ FJ －
CONTINUE
Z*Y/(1.000- P)
P = 0.500 -
40 CONTINUE
IF(U.GT. 0.0DO) P = 1.ODO~P
RETURN
NDRF0043
NORFO044
NORF0045
NORF0046
NORF0047
NORF0048
NORF0049
NORF0050
NORF0051
NORF0052
NORF0053
NORF0054
NORF0055
NORF0056
NDRI0057
NURF0058
NORF0059
NURFC060
NORF0061
NORF0062
NORI0063
NORF0064
NORF0065
NURF0066
GB 4086.1-83
SUBROUTINE NORXO(P,EPS.U,IER)INTEGER IER
DOUBLE PRECISION P,EPS,U
** PURPOSE **
PERCENTAGE POINT OF NORMAL DISTRIBUTION** ARGUMENTS **
ONENTRY
ON RETURN
LOWER PROBABILITY
REQUIRED PRECISION
PERCENTAGE POINT
ERROR PARAMETER
IER.NE.O INDICATES P.LE.O OR P.GE.1** REQUIRED ROUTINES **
DISTRIBUTION FUNCTION OF NORMAL DISTRIBUTION** ALGORITHM **
FOR P=O.5,
FOR P,NE.O.S, HITOTUMATU-S ITERATION METHOD IS USEO.INITIAL VALUE IS CALCULATED BY YAMAUTI-S FORMULA,U(P) = C*SQRT(Y*(2.0611786-5.7262204/(Y+11.640595))),WHERE
Y = -ln(P*(1-p)*4),
FOR P.GT.0.5,
C = 1,
C =-1,
FOR P.Lt.0.5.
INTEGER MN
DOUBLE PRECISION R.PP.ROOT.Y,DENS,DDENSIER 0
IF

U = 1.009*DSIGN(1.000,P-0.500)GOTO40
10O CONTINUE
IF (P .NE. 0.5DO) GO TO 20
U = 0.0DO
GOTO40
2O CONTINUE
INITIAL VALUE
Y ± -DL06(P*(1.0D0-P)*4.000)U ± DSQRT(Y*(2.0611786D0-5.7262204DO/(Y+11.640595D0)))IF P ,LT、0.500) U = -U
ITERATION
30DENS=DEXP(-0.500*U*U)*0.398942280401432678D0DDENS = U*DENS
CALL NDRFD(U,PP)
R = 2.0DO*(P - PP)
NORXO001
NORX0002
NORX0003
NORX0004
NORX0005
NORX0006
NORX0007
NORX0008
NORX0009
NORXO010
NORX0011
NORX0012
NORX0013
NORX0014
NORX0015
NORX0016
NORXQ017
NORX0018
NORX0019
NORX0020
NORX0021
NORX0022
NORX0023
NORX0024
NDRX0025
NORX0026
NORX0027
NORX0028
NORX0029
NORX0030
NORXQ031
NORX0032
NORX0033
NORX0034
NORX0035
NRX0036
NORX0037
NORX0038
NORX0039
NORX0040
NORX0041
NORX0042
NORX0043
NORX0044bZxz.net
NORX0045
NORXQ046
NORX0047
NORX0048
NORX0049
NORX0050
NORX0051
NORXO052
NORX0053
NORX0054
NORX0055
NORX0056
NORX0057
NORX0058
NORX0059
NORX0060
NORX0061
NORX0062
附加说明：
GB 4086.1--83
ROOT= DENS**2-R*DDENS
IF（ROOT.LE.O.ODO）R=DENS/DDENSIF (RODT .GT. 0.ODO) R = R/(DENS + DSQRT(ROOT))ＵＵ+Ｒ
MN = MN +1
IF（MN.EQ.10）GOTO40
IF(DABS(R).GT.EPS)GOTO30
4O CONTINUE
RETURN
本标准出全调统计方法应用标准化技术委员会提出。NORX0063
NORX0064
NORX0065
NORX0066
NORX0067
NORX0068
NORX0069
NORX0070
NORX0071
NORX0072
本标准用全国统计方法应用标准化技术委员会术语、符号和统计用表分委员会工作组起草。木标准士要起草人杨白强、魏公毅。191
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。