QJ 28A-1998 压力传感器静态性能不确定度计算方法 QJ28A-1998 标准下载解压密码：www.bzxz.net

1范围
中国航关工业总公司航关工业行业标准压力传感器静态性能不确定度
计算方法
1.1主题内容
本标准规定了压力传感器静态性能不确定度的计算方法。1.2适用范围
本标准适用于压力传感器在校准时的不确定度计算。引用文件
本章无条文。
3定义
不确定度
QJ28A-98
代替QJ28-87
与测量结果相关联的参数，表征合理赋予的被测量之值的分散性。对于传感器而言，它的不确定度由不可修正的系统误差分量和服从统计分布的离散分量所组成，取测量范围内校准点正、反行程中二者之和的最大值作为其不确定度。4一般要求
4.1环境
传感器静态校准时的环境条件，根据被校传感器的类型及等级由计量部门制定的检定规程作出规定。
4.2设备
校准系统（通常包括标准压力源、电源及传感器输出的测量仪表）的综合误差，一般应为被校传感器基本允差的1/10～1/5，至少应不大于1/3（特殊情况可为1/2）。4.3校准
传感器校准时，包括零点在内的压力校准点数K不应少于6点。校准的循环次数R不应少于3次。校准点数和校准循环次数的多少取决于被校传感器的等级和使用要求，通常K=611，R=35。每次校准共可获得2RK个校准数据。中国航天工业总公司1998—02—06批准1998—08—01实施
5详细要求
5.1传感器的校准曲线
QJ28A—98
设X为传感器的输入量（压力），Y为传感器的输出量（校准数据）。每个传感器有K个校准点X（i=1、2、K）。每个校准点均有R个正行程校准数据Y&i（j=1、2、R）和R个反行程校准数据Y（j=1、2、R）。按下面的公式求出各校准点的正、反行程校准数据平均值和总平均值：(1)
式中：Yi
(e+yn)
第i个校准点正行程校准数据的平均值；第i个校准点上第i次正行程校准数据；第i个校准点反行程校准数据的平均值；第i个校准点上第i次反行程校准数据；第i个校准点全部校准数据的总平均值。(3)
由各个Y。所连接成的线称为传感器的正行程校准曲线；由各个Y所连接成的线称为传感器的反行程校准曲线，由各个Y；所连接成的线称为传感器的校准曲线。5.2传感器的工作直线
为了实际使用的方便，往往用一条工作直线来代替实际的校准曲线。由它来反映传感器的输入和输出之间的关系。传感器的工作直线可用下面的特性方程表示：Y=a+bx....
式中：a一—工作直线在Y轴上的截矩；b工作直线的斜率。
传感器的工作直线是根据校准数据采用最小二乘法来确定的。根据校准数据，可按下列公式求得直线方程的截矩a和斜率b：XY
QJ28A—98
对于通常的等间隔校准。即X+1=X十h（h为传感器两相邻校准点的输入差值），可利用表1提供的公式简捷地求得b值。表1
校准点数K
b的计算公式
（5Y6+3Y5+Y4—Ys—3Y2—5Yi）/35h(3Y+2Y6+Y5—Ys—2Y2—3Y1）/28h(7Y+5Y+3Y6+Ys—3Ys—5Y2—7Y1）/84h（4Y。+3Y+2Y-+Y6—Y4—2Y—3Yz—4Y1）/66h(9Y10+7Yg+5Yg+3Y+Y6—Y5—3Y4—5Ys—7Y2—9Yi）/165h（5Yu+4Y10+3Yg+2Ys+Y—Ys—2Y4—3Ys—4Y2—5Yi）/110h为减少计算工作量，如有条件可采用具有统计计算功能的计算器或可编程序计算机来迅速地求得直线方程。
5.3传感器的静态基本性能指标
5.3.1非线性8
非线性是指在规定条件下，传感器校准曲线与工作直线的不一致性。在数值上用传感器校准曲线与工作直线间的最大偏差对满量程输出的百分比值来表示。计算公式如下：o
ALm×100%
QJ28A—98
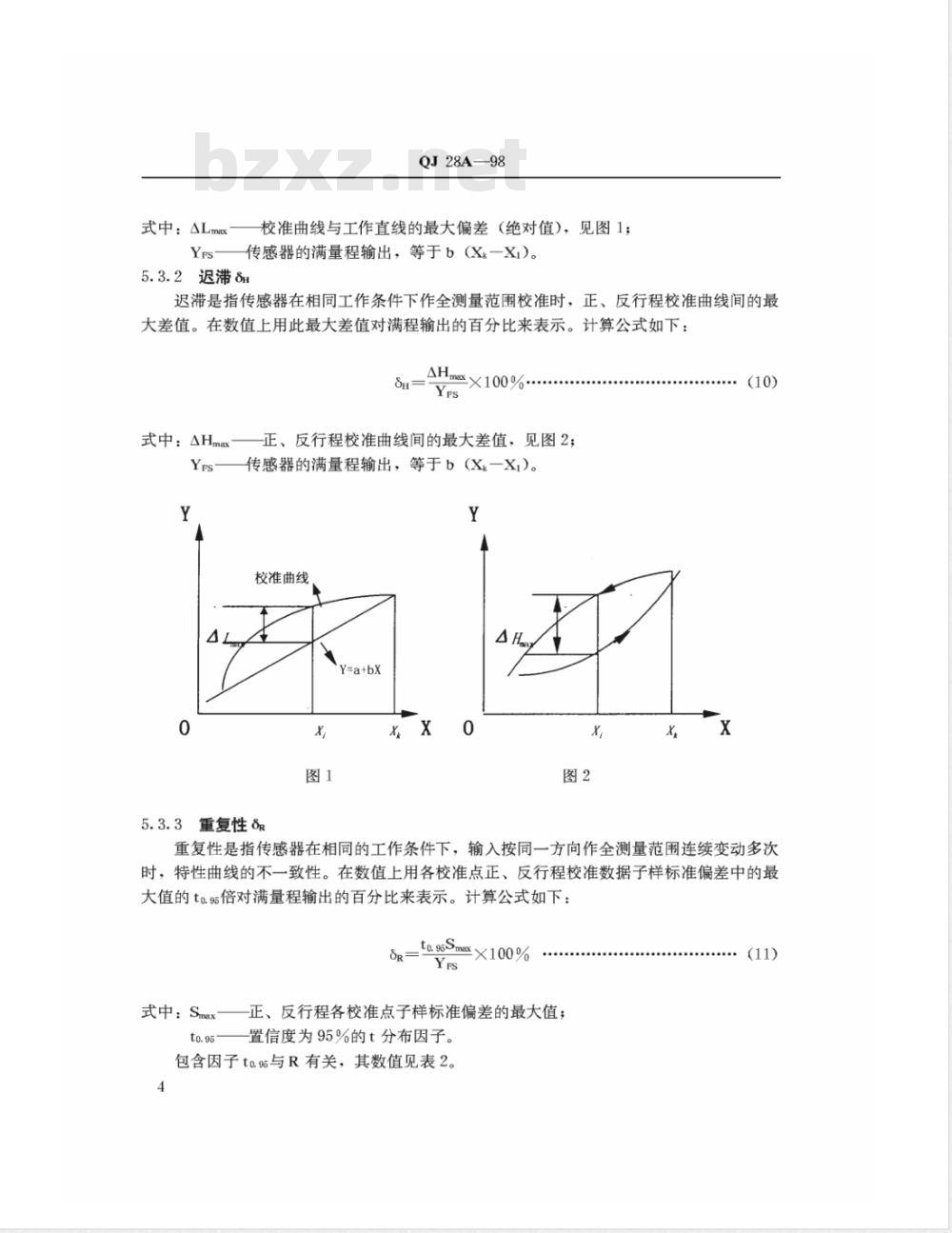
式中：ALmx校准曲线与工作直线的最大偏差（绝对值），见图1；Yrs传感器的满量程输出，等于b（X一X）。5.3.2迟滞8
迟滞是指传感器在相同工作条件下作全测量范围校准时，正、反行程校准曲线间的最大差值。在数值上用此最大差值对满程输出的百分比来表示。计算公式如下：AHmax
X100%：
式中：AHmx
正、反行程校准曲线间的最大差值，见图2；传感器的满量程输出，等于b（X一X）。Y
校准曲线
Y=a+bx
5.3.3重复性8R
重复性是指传感器在相同的工作条件下，输入按同一方向作全测量范围连续变动多次时，特性曲线的不一致性。在数值上用各校准点正、反行程校准数据子样标准偏差中的最大值的to.95倍对满量程输出的百分比来表示。计算公式如下：ta.9sSma
式中：Smax
正、反行程各校准点子样标准偏差的最大值；置信度为95%的t分布因子。
包含因子to.9与R有关，其数值见表2。4
标准偏差采用贝赛尔法计算。
QJ28A-—98
正行程第i个校准点的子样标准偏差S。为：(YaY&)2
反行程第i个校准点的子样标准偏差S为：(YaYa)
取上述Se和S（共2K个点）中的最大值Smx，按公式11计算传感器的重复性指标。5.3.4传感器的不确定度U
传感器的不确定度（或总误差）是传感器各校准点正、反行程的实际输出值相对于工作直线的偏差在规定的置信度下皆不超过的一个极限范围，见图3，其数值按下式确定：U=Maxm（Ba+to.gSei)，(Ba+to.9Sn）m式中：Max为选最大值的函数符号；Ba—第i个校准点正行程平均值与该值最小二乘值之差的绝对值；B—第i个校准点反行程平均值与该值最小二乘值之差的绝对值。通常，用相对不确定度U，来表示传感器的综合性能，其计算公式如下：U
计算举例
QJ28A—98
fo. 95 : s
Y=a+bx
压力传感器的静态性能不确定度计算举例见附录A（参考件）。6
A1工作直线的确定
QJ28A—98
附录A
计算举例
(参考件）
根据表A1的校准数据，计算出各校准点正、反行程校准数据的平均值及总平均值。A1.1工作直线的斜率
根据表A1中所列的各校准点校准数据的总平均值，按表1的计算公式（此处K=8，h=200）计算b值：
b=（7Y+5Y+3Y+Y—Y4—3Y—5Y2—7Y）/84h6.5659
斜率b也可按公式6计算，二者计算结果相同。A1.2工作直线的截距
根据各校准点的压力值X及其校准数据总平均值Yi，按公式7和8可求得文和Y：Y
CYi=5571.1
按公式5即可求得截距a：
a=Y-bX=5571.1-6.5659×700=975.0A1.3工作直线方程
根据已得出的a和b值，即可写出工作直线方程：Y=975.0+6.5659X
据此可得出各校准点的最小二乘直线，见表A1。传感器静态性能指标
压力Pa
正行程
反行程
正行程
反行程wwW.bzxz.Net
正行程
反行程
正行程
反行程
正行程
反行程
正行程平均值
反行程平均值
总平均值
最小二乘线值a+bx
线性差值
退滞性
正行程标准偏差Sc
反行程标准偏差Ss
正行程系统偏差Be
正行程系统偏差Se
Bet+to.9sSei
Ber+to.9Set
QJ28A—98
注：表中带*号的值是计算举例中所取值。非线性8L
根据表A1，求出各校准点校准数据的总平均值Y；与相应的最小二乘线性之值一各校准点的线性差值（取绝对值），然后取其中的最大值为传感器的最大线性差值，此处△Lmx=7.2，按公式9得：
ALm××100%=
×100%=0.08%
6.5659×1400
A2.2迟滞8
QJ28A—98
根据表A1的正、反行程的校准数据的平均值，得出各校准点的迟滞值，然后取其中的最大值AHmax=15.8，按公式10得：10%6.10%0.17%
A2.3重复性8k
根据表A1的计算数据，得出各校准点的正、反行程子样标准偏差中的最大值Smax7.42，本例中，因R=5，故to.95=2.776，按公式11得：to.96Sm××100%=
2.776X7.42
X100%=0.22%
A2.4不确定度U
根据表A1找出各校准点正、反行程中系统误差与to.95S之和（列于表A1最后二行）其中的最大者即为传感器的不确定度U。U=Maxm（B+to.95Sei)，(B+ta.95S）m9.3+2.776X7.4229.90
传感器的相对不确定度U.为：
×100%=91923×100%=0.33%
附加说明：
本标准由中国航天工业总公司七○八所提出。本标准由中国航天工业总公司七○八所负责起草。本标准主要起草人：项冀平、周辉。本标准主要审查人：郑石岩、蒋本雨、唐柏森、梁经才、王振祥。9
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。