本标准规定用样本估计总体的均值和方差，以及检验关于均值和方差的某些假设的方法。 GB 4889-1985 数据的统计处理和解释 正态分布均值和方差的估计与检验方法 GB4889-1985 标准下载解压密码：www.bzxz.net
本标准规定用样本估计总体的均值和方差，以及检验关于均值和方差的某些假设的方法。

1引言
中华人民共和国国家标准
数据的统计处理和解释
正态分布均值和方差的估计与检验方法Statistical Interpretation of dataTechniques of estimation and testsrelating to means and varlarcesof normal distributions
UDC 51$.28
GB 4889-85
1.1本标准规定用样本估计总体的均值和方差，以及检验关于均值和方差的某些假设的方法。对于成对观测值的比较参见GB3361一82《数据的统计处理和解释在成对观测值情形下两个均值的比较》。
1.2在所考虑的每个总体中，只有抽样单位是随机和独立地抽取时，使用这些方法才能有效。在有限总体的情况下，当总体的大小是充分大或抽样的比例是充分小（比如小于1/10）时，随机抽取的抽样单位可以认为是独立的。
1.8本标准适用于总体分布为正态分布的情形。如果总体分布偏离正态不大，样本大小不是太小时，下面叙述的方法依然近似正确，其近似程度对大多数实际应用是足够的。对表1，表3，表5和表7，样本大小应至少为5到10。对其他各表，样本大小应不少于20。
如果总体分布显著偏离正态，可以将变量变换成正态的或采用非参数检验方法。1.4总体的均值μ和方差的点估计分别由样本的均值义和方差S?给出。1.5在总体的均值μ和方差的区间估计中，置信水平1一α是置信区间包含被估计参数真值的概率。置信水平1～α值通常取0.95或0.99，即α=0.05或0.01。1.6在假设检验中，对双侧情形，显著性水平是在原假设成立时，拒绝这个假设的概率（第I类错误概率），对单侧情形，显著性水平是上述概率的最大值（第1类错误概率的最大值）。α0.05或α=0.01是依照使用者准备承受的不同风险而常用的值。因为在使用α=0.05时某个假设可能被拒绝，而在使用α=0.01时可能不被拒绝，所以采用“这假设在5%的水平上被拒绝”的提法，或在后一种情形采用“这假设在1%的水平上被拒绝”的提法。如果原假设不成立但被接受下来，就犯了第Ⅱ类错误。
1.7对于个别可疑的数据不能任意剔除或修正，具体处理办法见GB4883--85《数据的统计处理和解释正态样本异常值的判断和处理》。1.8在统计计算时，要给出观测值的来源和收集方法等有关信息。1.9在统计计算时，通过改变原点或单位常可使计算简化。1.10本标准系参照国际标准ISO2854《数据的统计解释一均值和方差的估算与检验方法》（1976年第一版）制订的。
国家标准局1985-01-29发布
1985-10-01实施
2计算的表格
总体的技术特性
抽样单位的技术特性
被剔除的观测值
统计项目
样本大小：
观测值的和：
≥x,=
给定值：
GB 4889---85
均值与给定值的比较（方差已知）表1
总体方差的已知值：
标准差：
显著性水平：
总体均值u与给定值μ。的比较
双侧情形：
如果{-μo「>（u-ai2l/n）
则拒绝总体均值与给定值相等的原假设单侧情形，
a，如果<μo-（u-an）α
则拒绝总体均值不小于给定值的原假设。b.如果x+（u,=aljn）
则拒绝总体均值不大于给定值的原假设说明：
U表示标准正态变量，u。值定义为a，
p(U因为U的分布关于零对称，u。=l-α'所以有P(U>u.)=1-α
Ma/= - w[-a/2
双侧情形
GB 4889-80
-α/2单侧情形
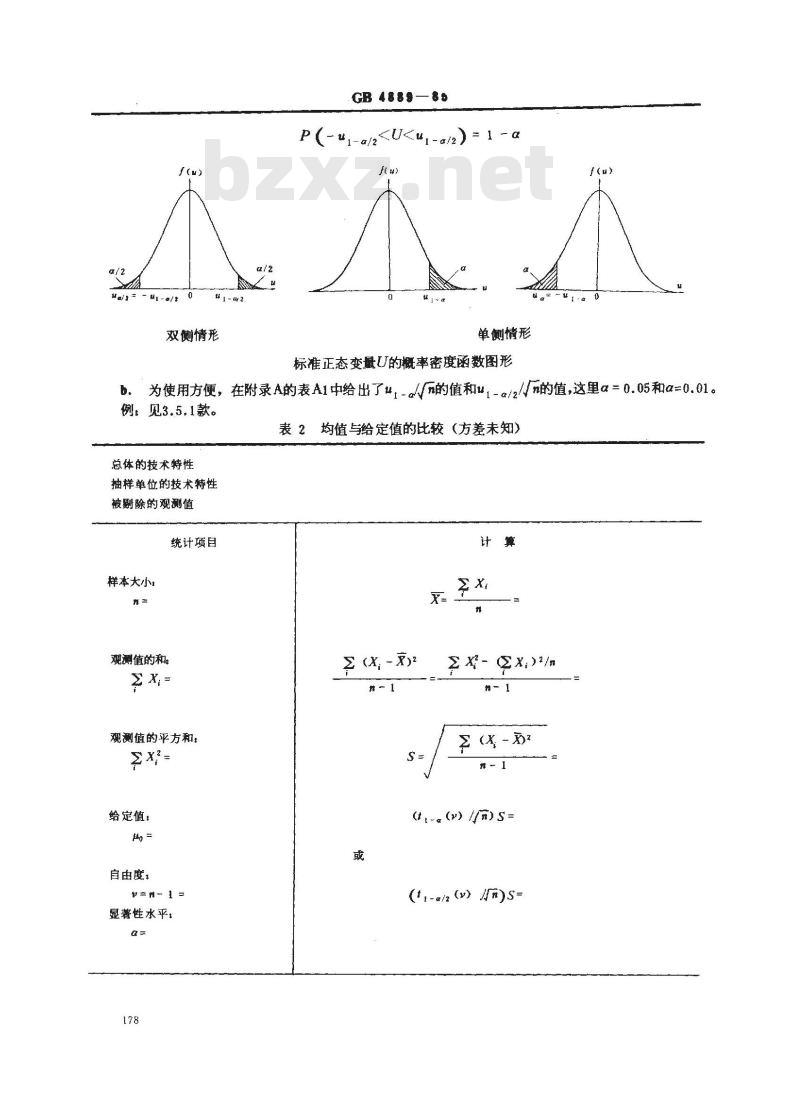
标准正态变量U的概率密度函数图形广(
b．为使用方便，在附录A的表A1中给出了u1-α//n的值和ul-a/2//n的值,这里a=0.05和α=0.01。例：见3.5.1款。
表2均值与给定值的比较（方差未知）总体的技术特性
抽样单位的技术特性
被剔除的观测值
统计项目
样本大小：
观测值的和：
观测值的平方和：
给定值：
自由度，
v=n-1-
显著性水平，
(X, -)2
E-Qx)3/n
(t+-a (v) I/n)S=
(tt-a/z()/)s=
总体均值μ与给定值的比较
双侧情形：
如果/ X-μ ≥(1-a/2() /)
则拒绝总体均值与给定值相等的原假设。单侧情形：
a 如果X<μo-(t,-() I)
则拒绝总体均值不小于给定值的原假设。b.如果x>μo +(t1-α()/n)s
则拒绝总体均值不大于给定值的原假设说明：
GB 4889-85
续表2
a。t（）表示自由度为v=n-1的t变量。t。（）值定义为P(t (v) 因为t（v）的分布关于零对称，t。（\）=-t，-α（），所以有p(t(v) >t(v)) = 1 -α
P(-t1-a/2 (u) ta/2 (v)
a(+(u)
双侧情形
tj-/()
单侧情形
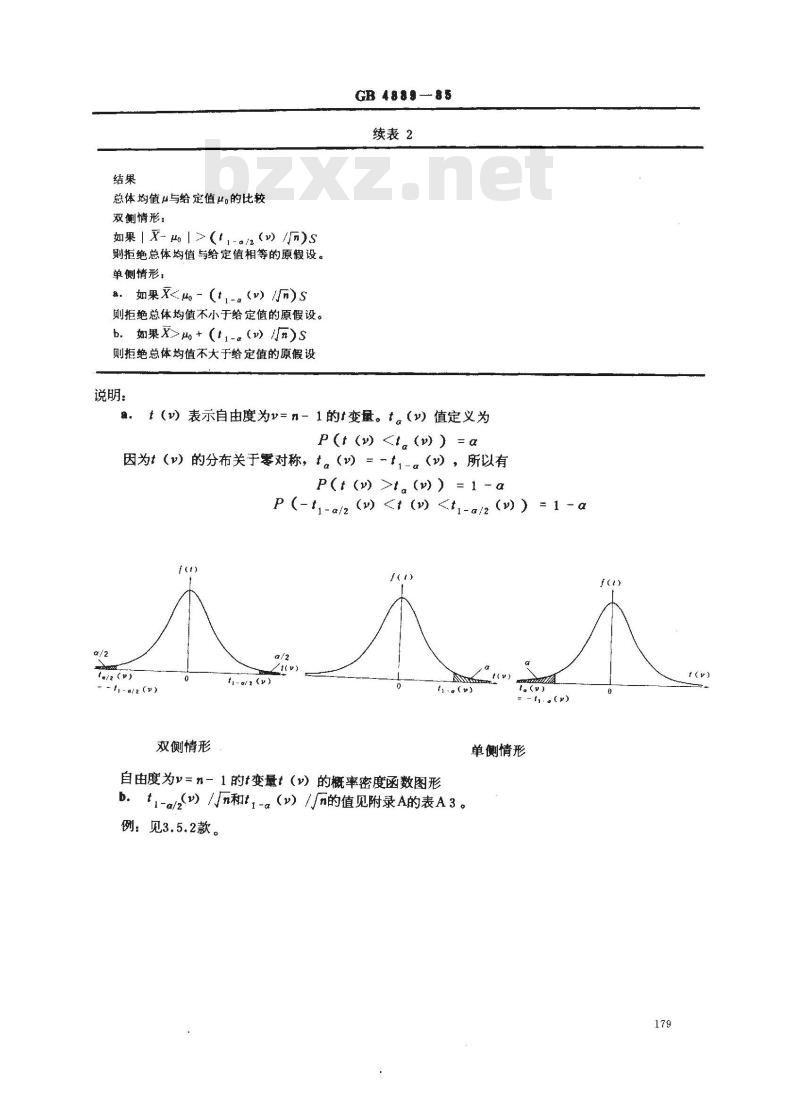
自由度为=n1的t变量t（）的概率密度函数图形b.
ti-αa/（）//n和t1-α（v）//n的值见附录A的表A3。例：见3.5.2款。
总体的技术特性
抽样单位的技术特性
被谢除的观测值
统计项目
样本大小，
观测值的和；
总体方差的已知值：
置信水平，
总体均值u的估计
GB 4889--85
表3均值的估计（方差已知）
(ui-α/fn)g =
(u-a/2/ )a
双侧置信区间，
X-(u1 - a/ 2//m)o<μu或 μ>X-(ui-a//n)a
说明：
．u。值定义见表1中“说明a”
b，“,-a /2/n和u1-α/ n的值见附录A的表A1。例：见3.5.3款。
总体的技术特性
抽样单位的技术特性
被别除的观测值
统计项目
样本大小
观测值的和：
观测值的平方和
自由度：
v-n-l=
置信水平，
结 果
总体均值从的估计
GB 48B9-85
均值的估计（方差未知）
(X-X)2
EX -(2X)2/n
(-x)2
(t1-a(v) /n)s=
双侧置信区间，
X-(t 1-a/2 (v) //n)s<μuμ>X-(t-(v)/)s
说明：
(t1-a/2 (v) /fn)S=
t。（v)值定义见表2中“说明a”。t-a/2(）／/n和1-α（v）／/n的值见附录A的表A3。b.
例，见3.5.4款。
总体1的1
总体2的」
总体1中1
总体2中享
样本1中［
样本2中」
样本大小·
观测值的和；
技术特性
抽样单位的技术特性
被剔除的观测值
统计项目
第一个
总体方差的已知值：α=
显著性水平，
结 果
两个总体均值的比较
GB 4889-85
表5两个均值的比较（方差已知）第二个
r-aag=
双侧情形，
如果/2
则拒绝两个均值相等的原假设。单侧情形：
a 如果X,则拒绝第一个均值不小于第二个均值的原假设。b）如果i-oa
则拒绝第一个均值不大于第二个均值的原假设说明：
。“。值定义见表1中“说明a”b。 ui-a/ 和u1-。的值由附录A表A1的n=1那行得出。例；见3.5.5款。
GB4889—85
表6两个均值的比较（方差均未知，但有理由认为相等或近似相等，否则不能用）关于两个总体方差相等的假设，可用表11所示方法来检验总体2的！技术特性
总体1的1
抽样单位的技术特性
样本1中
被剔除的观测值
样本2中
统计项目
第一个
样本大小
观测值的和：
观测值的平方和：
第二个
MX21 =
自由度：V=+n2-
显著性水平：
两个总体均值的比较
F (X1: -X)2+2 (X2i-X)2
- X+E X2
双侧情形，
如果,-X,>-a/() S
则拒绝两个均值相等的原假设。单侧情形，
a)如果 X,Xf-（v)S
则拒绝第一个均值不小于第二个均值的原假设。b）如果X>Xz+t-α（) S
则拒绝第一个均值不大于第二个均值的原假设说明：
Z (X, -X)2+2 (X2 -Xx,)z
ni+n2 - 2
1a() Sg
-a/2(v)Sa-
．t。（）值定义见表2中“说明a”。b.}-a/2(v）和t{-α（）的值见附录A的表A2。例：见3.5.6款。
总体1的1
技术特性
总体2的」
总体1中
总体2中」
样本1m
样本2中』
样本大小，
GB 4889--85
表7两个均值之差的估计（方差已知)抽样单位的技术特性
被剔除的观测值
统计项目
第一个
观测值的和：≥X，=
总体方差的已知值：
暨信水平，
两个总体均值μ,和2之差的估计=
第二个
双侧置信区间：
(X -X) \u1-a/20a<-μa<()-X) +ul-a/20d单侧置信区间：
μ - μe<(X-X,) + u-ad
或μμ>（-）-od
说明：
u。值定义见表1中“说明a”，
b．ul-α/2和u1-α的值由附录A表A1 的n=1那行得出。例：见3.5.7款。
u_-αda=
w1-a/20d =
GB 4889-85
表8两个均值之差的估计（方差均未知，但有理由认为相等或近似相等，否则不能用）关于两个总体方差相等的假设，可用表11所示方法来检验总体1的1
技术特性
总体2的了
总体1中心
抽样单位的技术特性
总体2中了
样本1中！
被除的观测值
样本2中
统计项目
第一个
样本大小，n，=
观测值的和: X：=
观测值的平方和
第二个
自由度，=n, +n2 2
量信水平，
两个总体均值μ和μ2之差的估计X-x,=
双侧量信区间:
(X -X)3+(X2 -X22
+ -22=
(X: -X)2+E (X2, -X,)2
nj + n2 - 2
ti-α(v) S=
11-a/2(v) S4 =
(X,~X) -t+-a/2(v) S<μ-μ<(X, - X,) +-a/2(v) Sa单侧量信区间;
μ-μ<(X,- X,)+t,-α() Ss
μ>(）)t-() S
说明：
。。（v）值定义见表2中“说明a”b。 1~a/2（）和 t-。（）的值见附录A的表A2。例，见3.5.8款。
总体的技术特性
抽样单位的技术特性
被剧除的观测值
统计项自
样本大小，
观测值的和：
观测值的平方和
给定值：
自由度
=n- 1=此内容来自标准下载网
显著性水平，
总体方差与给定值的比较
双侧情形：
(X X)2
(X, -X)2
GB 4889-85
表9方差与给定值的比较
E(X, -X)2=Ex3
(X, -X)2
i--(v) =
xz(）
x-a/2(v) =
a/2（）
则拒绝总体方差等于给定值的原假设。单侧情形，
(X -X)2
GB 48899-85
续表9
>xi-a）
测拒绝总体方差不大于给定值的原假设。b)
(X-X)2
则拒绝总体方差不小于给定值的原假设说明：
2（）表示自由度为的2变量，（）值定义为a，
p(x2()所以有 P(×2()>×()）=1-α
p(×/2(）×2(）<-a/2()）=1-αftx2)
双侧情形
Xi-a/2(v)
单侧情形
自由度为1的变量2（）的概率密度函数图形在附录A的表A4内，对α=0.05和α=0.01，给出了×（），×-α（)，×2a/2（v）和b.
x-a/2(v)的值。
例：见3.5.9款。
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。