HG 3104-1989
基本信息
标准号: HG 3104-1989
中文名称:橡胶试验数据分布类型检验规定
标准类别:化工行业标准(HG)
英文名称: Rubber test data distribution type inspection regulations
标准状态:现行
出版语种:简体中文
下载格式:.rar.pdf
下载大小:440641

标准分类号
出版信息
标准价格:15.0 元
相关单位信息
标准简介
HG 3104-1989 橡胶试验数据分布类型检验规定 HG3104-1989 标准下载解压密码:www.bzxz.net
标准图片预览



标准内容
UDC 678. 4. 01
中华人民共和国国家标准
GB1117989
调整为: HGh 3104 -f8
橡胶试验数据分布类型检验规定Rubber-test rule for distribution type of testing data1989-03-31发布
国家技术监督局
1990.01-01实施
中华人民共和国国家标准
橡胶试验数据分布类型检验规定Rubber-testrulefor distribution type of testingdata1志题内容和适用范围
GB 11179—89
本标准规定了用方法检验像胶试验数据分布类型的基本程序。根据本标准可以确定产品质量指标和经济指标的分布类型,亦可确定橡胶或橡胶制品试验数据的分布类型。本标推适用于检验橡胶试验观测值,观测值进行函数变换后的数据及随机数据经验分布与理论分布类型的拟合度。
2引用标准
GB 528硫化橡胶拉伸性能的测定GB3187可靠性基本名调术语及定义GB3358统计学名词及符号
GB4882数据的统计处理和解释
正态性检验
3符号
H…-原假设;
n——样本大小;
,X。—样本的n个顺序统计量观测值,R(X,)——观测值为又,时,理论分布的函数值;检验的显著性水平;
-检验所用的统计量;
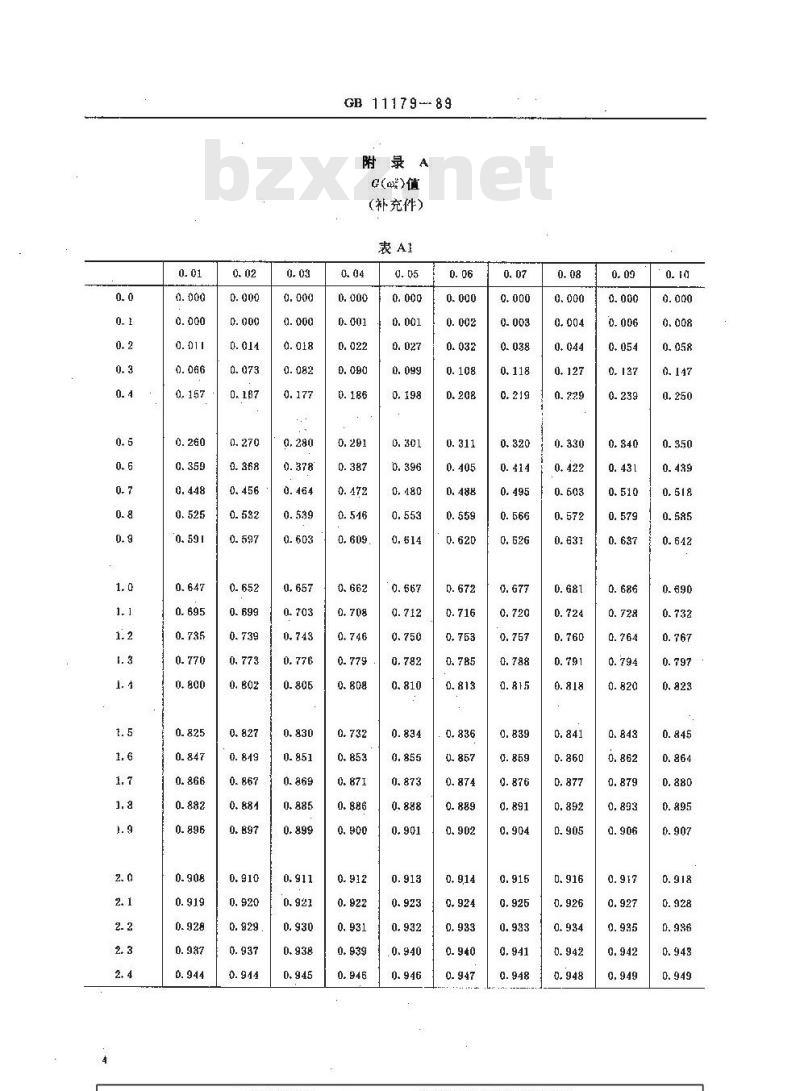
G(a)—值的分布函数。其数值见附录A。4应用条件
4-1当怀疑样本来自某个已知的总体分布时,应进行相应分布类型的检验。4.2检验方法可用于各种分布的检验,抽样必须保证随机性,随机变量的观测值应在相同条件下取得。被观测的样本必须米自向一总体。4.3样本大小不得小于50。
4.4当需要由样本估计众数、加权平均值或如权标准差时,必须把样本等距离分组,组数取决于样本大小。与样本大小的关系是:
Rw 50~99
#- 140-199
中华人民共和国化学工业部1989-03-10批准710-15
r=1518
1990-01-01实施
5实施步骤
n—1 000
GB 11179—89
r— 1820
7= 35~~40
5.1给出Ho:样本米自某个已知理论分布。5.2将观测值排列为顺序统计量
X+X..*,X.
5.3计算理论分布函数值
(j-1,2.**)
5.4按式(2)计算品:
f(x,)dx
22iInF(X) +
1-2j-1
In(—F(X,))
(2)
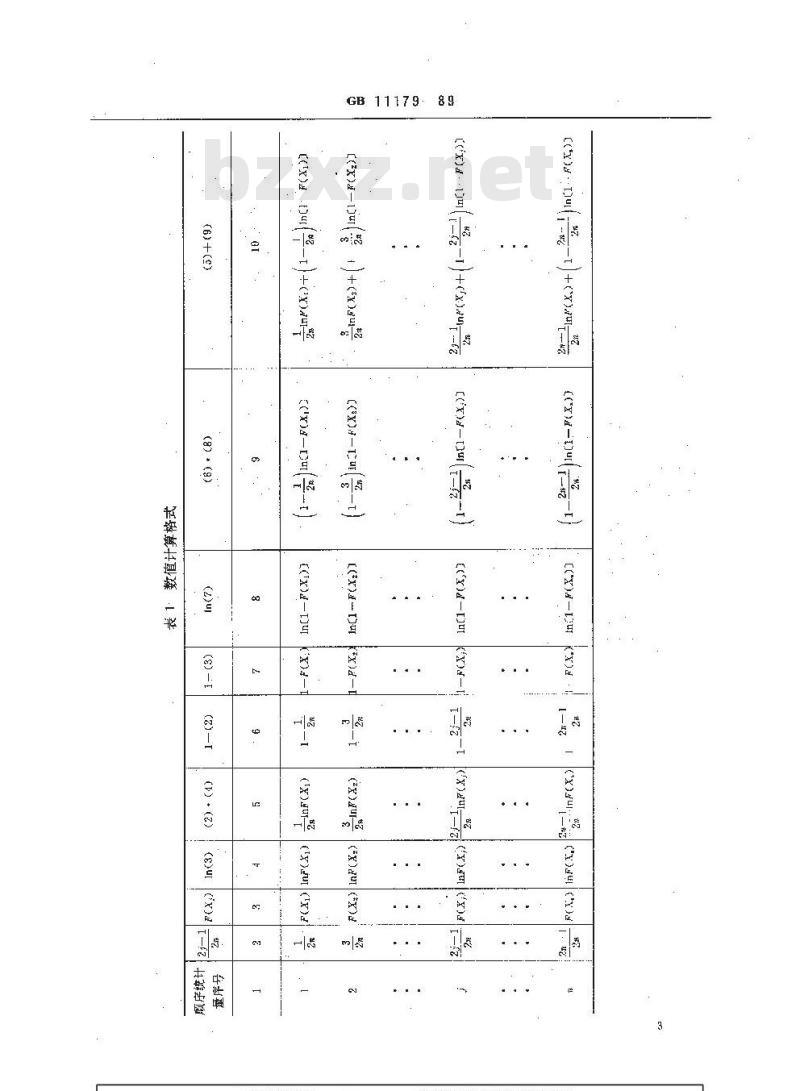
让算时按表1填满数据。表1中的中间结果计算到五位有效数字,最后结果保留三位有效数字。将表1第10列累加起来,按公式(2)计算得到需。5.5在附录A中与相应的分布函数值(@)。5.6取显著性水平在=0.2。
5.7作出判断:
如果Q()≥1,则拒绝H即拒绝经验分布与理论分布相符合的假设如果()<1一,则接受这种假设。
按o检验正态分布的举例见附录B;BASIC程序见附录C。2
GB1117989
( (-t)+
cexa-tia
)+ex)u
(6)+()
(ca-(e-t)
(x)-(-t)
Eex)&-utkxd-i
GB 11179~89
附录A
G(磁)值
(补充件)
0. 09
GH11179
续表A1
附录B
(参考件)
选用天然橡胶硫化胶试样,按GB528的4号裁刀得到一个&=57的拉伸强度(单位:MPa)的样本。用员方法检验总体是否服从正态分布。B1给出I:样本来自止态分布,
B2将观测值排列为顺序统计量(见表B1)。B3按观测数据计算正态分布的参数估计量X,8和所有的理论分布函数值:肉
S--1. 1237
(j-1,2,-,57)
分别把顺序统计量序号;和顺序统计量X,的理论分布值F(X)填入表1的第1列和第3列,再按表1的第2列及第4至10列各计算式计算,填入对应结果构成表32,其中的第10列数值相加得—28.715.
— 57 — 2 × (- 28. 715)
B4给出显著性水平a-0.2
B5套附录A得Q(o%)-G(0.13)=D.1771—= 0. 8
G(1一
接受所。:原样本来自正态分布的总体。5
.0. 044
0·482
0. 002 99
0. 006 53
0. 020 81
e. (55 61
表 B1
GB 11179—89
排成顺序统计量的原始数据
用表 B1 的数据按表 1 中各计算式计算所得结果5
5. 811 99
--5. 030'87
—3.872 46
—0.050 98
:0.169 84
-2, 889 44 0. 177 42
—2. 713 39
0. 956 11
0. 938 60
—0.214-22
—2. 225 36
- 0. 214 73
0. 125 45
--.2. 075 840, 236 72
0. 165 94
0. 189 05
0. 214 04
0.903 -51
1. 796 11 -0. 236 33
:-1. 665 74
-0.248 40
--1. 541 59
—0. 256 93
0. 833 33
0. 997 01
0. 993 47
0. 933 69
0. 891 97
0. 874 55
心.810 95
—0.003 00
—0.00297
—0. 006 38
0.053 95.
—0. 138 77
— 0. 020 10 : —0. 189 95
0. 021 03
0. 057 210. 053 700. 231 12
0. 068 61 - 0. 063 20 — 0. 277 41 0. 114 32
- 0. 103 29
—0. 318 02
0. 134 050. 118 76
—0.35548
-0. 181 46
0. 157 58
—0.39391
0. 209 55
-0.178 30
0. 785 96
5 -0. 200 710. 457 64
0. 240 851. 423 57 0. 262 240. 816 79 0. 759 150.240 85
0. 269 40
0. 269 40
1. 423 57-0. 287 21
1. 423 57 0. 312 19
1. 311 57 0. 310 64
1. 311 57 0. 333 65
1. 311 57 -- 0. 356 66
1. 311 57 :0. 379 67
0. 745 61
0. 331 13 m 1. 105 25 0. 339 330.363 96
1. 010 700. 328 03
~1. 010 70-0. 345 77
0. 363 96
0. 432 49
0. 432 49
0. 467 67
0. 467 67
0. 467 67
1.010 70-0.363 50
—1. 010 70 :0. 381 23
. 0. 330 87
0. 838 200. 345 57
- 0. 838 200. 360 28
—0. 759 99
0. 759 99
—0.75999
—0. 339 99
—0.353 33
—0. 366 66
0. 675 44
0. 640 35.
0. 622 81
0. 605 26
0. 587 72.
0. 552 63
0. 759 15
.0.730 60
0. 668 87
0. 636 04
0. 636 04
0. 567 51
0. 567 51
:0.532 33
0:53233
—0.275560.224 80.-0.487-04
- 0. 275 56
..- 0. 219 96
—0. 507 18
-0. 275 56 —0. 215 13
0. 319 88-- 0. 239 54
-0.550 18
: 0. 234 04
—0.228 53
-0. 313 880. 223 02
-0.567 68
-- 0. 602 69
— 0. 402 16 -- 0. 278 69
- 0.618 02
.*0. 452 50--0. 305 64
0. 452 50 0. 297 70
:-0. 452 500.289 76
0. 452 50— 0. 281 82
0. 566 50 0. 342 88
0. 566 50-- 0. 332 94
0. 633 67
0. 643 46
—0.65326
0. 663 05
—0. 673 75
0. 678 51
0. 566 50: 0. 323 00
D. 630 50 0. 348 43
— 0. 337 37
-- 0. 326 31
—0. 688 43
一心.69心70
0. 692 97
0. 503 11
0. 573 64
0. 573 64
0: 641 88
0. 674 51
0. 674 51
0. 815 14
0. 815 14
0: 815 14
0. 815 14
0. 837 91
0. 837 91
GB 11179-: 89
续表 B2
— 0. 686 94
—0.343 17
— 0. 618 92
-0. 618 92
— 0. 618 92
0. 500 00
-0. 320 32
—0.33118
0. 342 04
—0.55576
-0. 316 88
0. 443 36 0. 268 35
0. 393 770. 245 24
- 0. 393 770. 252 15
— 0. 259 06
-0. 393 77
—0.23529
—0. 348 31
0. 306 89
— 0.212 67
0. 269 22
— 0. 191 29
0. 235 12
—0,20440
0. 152 40
0. 204 40-0. 155 99
0. 204 40 --0. 159 57
—0.16316
- 0. 176 B4 - 0. 141 26
-0. 176 ±4 -0.147 37
— 0. 152 25
—0. 129 54
-- 0. 152 25 0, 132 21
0. 447 37
0. 359 65
0. 342 11
0. 324 56
0. 289 47
.0. t84 21
0. 149 12
0. 131 58
-- U. 152 250. 134 89
0. 858 78
—0. 137 56
0. 152 25
-0.130 41
0. 120 11
0. 894 81 : -0. 111 11
— 0. 104 29
U. 955 18
0. 962 97
-0. 045 86
-- 0. 037 74:
0. 096 49
0. 078 95
0. 061 40
注:对正态分布检验,除用本方法外,亦可采用GB4882。7
0. 496 89
0. 461 48
0. 461 48
0. 358 12
0. 326 49
心.32549
:0. 294 14
0. 184 86
0. 184 86
0. 184 85
0. 162 09
0. 141 22
0. 141 22
0. 1-41 22
0. 122 26
0. 044 82
(0. 037 03
附录C
\检验的BASIC程序
(参考件)
- 0. 699 39
— 0. 349 70
0.773 330. 373 10
0. 773 33
—0.359 53
—0. 773 33
0. 345 96
0. 852. 46 -0. 366 41
-0.852 46
-0.351 45
-1. 026 88 0. 405 35
0. 603 17
-- 0. 690 71
0. 688 00
0. 683 29
0. 678 09
1. 122 42-0. 423 37
0.668 61
1.122 42 0, 403 68 0, 655 831. 122 420. 383 99
—1. 223 69—0. 397 16
1. 330 79 0. 408 57
- 0. 621 25
— 0. 417 95
1. 443·83
1. 562 92 -0. 425 01
1, 688 16 0. 429 41
—-0.596 19
1. 688 16 . - 0. 399 83
—0. 555 8 1
1, 688 16..0. $70 21
..0. 529 78
—1. 688 16 -0. 340 59
—0.503 75
1. 819 62 --0. 335 19 —0, 479 46-1. 819 62 - 0. 303 27 - 0. 450 64-1. 957 41
-0. 291 89
-- 0. 421 44
1. 957 41 0. 267 55 ~ 0. 389 771. 957 41 0. 223 21 ( 0. 358 10 1. 957 41
0. 188 87
—0. 165 92
—0.32643
—0. 286 03
—0.212.59
- 0. 136 19 -- 0. 180 03
—3.105 06
—3. 105 06
0. 081 :71
0. 126 36
0. 066 32
本程序用方法检验样本的正态分布与双重指数分布,1480~1490语句是留作添写其他分布计7
GB 1117989
算语句的位置。此外,本程序以人机对话式输入分组后给出直方图。源始数据是以TXT为后缴的顺序文件给出的。附录人中的待查数据也是一个数据文件,并命名为A,DA。程序能自动查出对应的表值,当所查数据超出表中的范画时,程序可自动算出该值并打印出米,10 WJDTH LPRINT 132
20 CLS:PRINT TAB(20)
30 PRINTTAB(20)
40 PRINT
“数据分布类型检验总菜单”
50PRINTTAB(5)“1.输入原始数据\,:PRINTTAB(46)“2.构成顺序统计量”60PRINTTAB(5)*3.打印直方图”;70PRTNTTAB(46)“4.2检验\,:PRINTTAB(5)80 PRINT\.PRINT
90INPUT“请选择编号执行对应操作”,BH100ONBHGOSUB120,250,310,710,1600110 GOTO 20
“6.结束”
“输入数据个数”,K:INPUT“输入 TXT 文件名”,Q$120 CLS.INPUT
130 DIM X(K),A(K,11).:OPEN \C.\+Q $ +\.TXT FOR INPUT AS I140FORI=1TOK:INPLT41,X(I).NEXTI.CLOSE#1150 XBA=0:SIGMA=0
160 FOR I=1 TO K
170 XBA=XBA+X(1)
180 NEXT1
190XBA-XBA/K
200 FOR1--1TOK
210SIGMA=SIGMA+(X(I)-XBA)*(X(1)-XBA)220 NFXTI
230 SIGMA=SQR(SIGMA/(K-1))
240 RETURN
250CLS,PRINT“正在排序”
260FORKK=1TOK-1
270 FOR NN=I TO K-1
280 IF X(NN)) X(NN+1) THEN SWAP X(NN),X(NN + 1)290 NEXT NN,KK
300 RETURN
310 CLS:INPUT
320 NH-1000
“输入分组个数\,R:H#一(X(K)一X(1))/R330 IF QI$=\Y\
OR BH=3 THEN ERASE S,ZZ
340 DIM S(R),ZZ(R)
350 FOR RR -1 TO R
360 S(RR)=0
370 ZZ(RR)-X(1)+(RR-0. 5) *H *380 NEXT RR
390 FOR KK-1 TO K
400 FOR RR=1 TO R
GB 11179-- 89
410 F X(KK)<--X(1)+RR *H#+0. 001 AND X(KK)) =X(1)+(RR-1) *H# 0. 001THFN 420 ELSE 440
420 S(RR)-S(RR)-+ 1
430 GOrO 450
410 NEXT RR
450 MEXT KK
460 F-s(1)
470 FORRR-1TOR
480IFS(RR))=FTHEN49DELSF510
490 F=S(RR)
500 R1--RR
610 NEXT RR
520 M0=X(1)(R1-1)*H# +H# * (S(R1)-S(R1-1))/(2+S(RI)-S(R1-1)—S(R1+1))530MZ=X(1)+(R—0.5)*H#
540 MZZ=2. 5/(MZ-M0)
550 FOR RR=1 TO R
“####.###\,X(I)+(RR—1)*H#;.PRINT.560PRINTUSING
“####.###\,X(I1)+RR*H#:PRINT USING“###\,USING
:PRINT
)0THEN580ELSEPRINTUSING“#########”,ZZ(RR):GOTO570 IF S(RR)<
580 PRINT USING *# ## ##. ####\;ZZ(RR);590 FOR NN=1 TO S(RR)
600 PRINT TAB(40+2* (NN.--1)) \\670 IF NN-S(RR) THEN PRINT \620 NEXT NN
630 NEXT RR
640INPUT“打印这幅直方图吗?Y/N”,Q3$650 IF Q3 $ -\y\ THEN Q3$ -\y\660IFQ3$-“Y\THENGOSUB1500
670INPUT‘重新分组吗?Y/N,Q1$680 IF Q1 $=\y\ THEN Q1 S -\Y\690 IF Q1 $ -*Yn THEN 310
700 Q1$--“Y\.RETURN
710 CLS
720PRINT\使用 \法检验橡胶物理试验数据的分布类型是普遍有效的,这里仅给出止态分布与双重指数分布检验,并在1380--1400处留有检验其它分布类型的接口”730 PRINT*
740 PRINT“1 正态分布”
750PRINT“2双重指数分布”
760FRINT“3其它分布\
770PRINT“4检验结束”
780PRINT“\,INPUT\请按序号选择”,BH2790 F BH2=4 THEN 1600
800FOR1-1TOK
GB 1117989
810 A(1,1)=-I:A(T,2)=(2*1-1)/(2*K)820 0N BH2 G0SUB 1350,1450,1480,1600830 A(T,3)=A1:A(I,4)-L0G(A(1,3)):A(1,5)=A(I,2)*A(I,4),A(I,6)=IA(I,2)840 A(I,7)-1—A(I,3):A(I,8)-L0G(A(1,7)):A(I,9)-A(I,6) A(I,8):A(1,10)=A(I,5)+A(I,9):A(I,1)-X(0)
850 NEXT 1
860 SUM-Dwww.bzxz.net
870FOMM-1TOK
880SUM=SUM+A(M,10)
890 NEXT M
900OMEGA=INT((-K2*SUM+0.005)*100/100!910 FOR I-1 TO K
920PRINTUSING“###”,A(1,1);:PRINTUSING“##.###\;A(I,2);930 PRINT USING“##. #####\;A(I,3),+PRINT USING *###.#####\,A(I,4);940 FRINT USING “###.#####\;A(I,5);:PRINT USING *##.#####\,A(I,5);950 PRINT USING *###、####*,A(I,?);:PRINT USING *###. #####\A(I,8)
960PRINTUSING“###.#####”;A(I,9):PRINTUSING“###,#####”A(1,10) ;
970 NEXT I
980LPRINT“?一”LPRINTUSING“###、##”OMEGA990 CODE% = 100+DMEGA
1000 IF CODE%)295 THEN 1010 ELSE 12601010 SS=0
1020 FOR JJ=0 TO 6
1030 IF JI=D THEN A1-1;GOTO 11301040FJJ=ITHENAI-0.5:GOTO11301050 FZ-JJ-0.5
1060 FM-JJ
1070 A1=F7./FM
1080FORI-JJTHEN2STEP-1
1090 FZ-FZ—1
1100 FM--FM-1
1110 A1=A1+FZ/FM
1120 NEXT 11
1130B1=(—1)^JJ*(4*JJ+1)*EXP((—9.87202324#*(4*JJ+1)/(8*OMEGA)))1140 IF ABS(B1) <1E-D9 THEN 1310I150 DBF FNPL(Y)--EXP(OMEGA/(8 * (Y * Y+1))-*OMEGA))
1160 N=1000
1170 H-500/N
1180 S0. 5 * (FNPL(0)—FNPL(1000))10
-((4 * JJ+1) * 3. 1415926# * Y) ~ 2/(81190FORL=1TON
GB 11179--89
1200 S=$+2*FNPL((2*L—1) *H)+FNPL(2*L* H)1210 NEXT I,
1220 CI=1000 *S* 2. 506628/(3 *N* 0MEGA)1230SSSS+AI*BiC1
1240 NEXT JJ
1250 GOTO1310
1260 OPEN“A;DA\AS 2 LEM=241270TIELD#2,8ASN$.8ASA$
1280 GEI #2,CODE%
1290 SS=VaL(A$)
1300 CLOSE
I3I0 LPRINT \Gα?)=\, :LPRINT USING “#, ###\,SS1320INPUT“还作检验吗?Y/N”,Q2$ 1330 F Q2$ -*y\ Then Q2$ --\y\1340 IF Q2 $ -\Y\ THEN. 710 FISE RETURN1350 B=(X(I)—XBA)/SIGMA
1360 C-—6
1370 NI=50
.1380H--(B-C)/(2*NI)
1390 S=0.5* (EXP(—C*2/2))(EXP(—B~2/2))/2.5066282#1400 FOR L- 1 TO NI
: 1410 S=S + 2 *EXP(-(C+(2*L-1) * H) ~ 2/2)/2. 5066282# +EXP(-(C+2 * L *H) 2/2)/2.5066282#
1420 NEXT L
1430 A1=(B—C)*S/(3*N1)
1440RETURN
1450B=
-EXP(MZZ8(X(I)-M0))
1460 A1=I--EXP(B) : IH A11 THEN AI -- 0. 999991470 RETURN
1480REMA1一待检验的某种分布的概率值1490 REMRETURN
1500 FORRR-1TOR
1510 LPRINTUSING“####.##±\,X(1)+(RR-1)*H#:.LPRINT“####.###\,X(1)+RR*H#;:LPRINT USING“###”LPRINT USING
1520 IF S(RR) < >0 THEN 153D ELSE LPRINT USING “# ####.####*;ZZ(RR).GOTO1580
1S30LPRINTSING“####,####”ZZ(RR)
1540 FOR NN=1 TO S(RR)
1550 LPRINT TAB(40+ 2 * (NN-1));\\1560IFNN-S(RR)THENI.PRINT
1570 NEXT NN
1580 NEXT RR
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。
中华人民共和国国家标准
GB1117989
调整为: HGh 3104 -f8
橡胶试验数据分布类型检验规定Rubber-test rule for distribution type of testing data1989-03-31发布
国家技术监督局
1990.01-01实施
中华人民共和国国家标准
橡胶试验数据分布类型检验规定Rubber-testrulefor distribution type of testingdata1志题内容和适用范围
GB 11179—89
本标准规定了用方法检验像胶试验数据分布类型的基本程序。根据本标准可以确定产品质量指标和经济指标的分布类型,亦可确定橡胶或橡胶制品试验数据的分布类型。本标推适用于检验橡胶试验观测值,观测值进行函数变换后的数据及随机数据经验分布与理论分布类型的拟合度。
2引用标准
GB 528硫化橡胶拉伸性能的测定GB3187可靠性基本名调术语及定义GB3358统计学名词及符号
GB4882数据的统计处理和解释
正态性检验
3符号
H…-原假设;
n——样本大小;
,X。—样本的n个顺序统计量观测值,R(X,)——观测值为又,时,理论分布的函数值;检验的显著性水平;
-检验所用的统计量;
G(a)—值的分布函数。其数值见附录A。4应用条件
4-1当怀疑样本来自某个已知的总体分布时,应进行相应分布类型的检验。4.2检验方法可用于各种分布的检验,抽样必须保证随机性,随机变量的观测值应在相同条件下取得。被观测的样本必须米自向一总体。4.3样本大小不得小于50。
4.4当需要由样本估计众数、加权平均值或如权标准差时,必须把样本等距离分组,组数取决于样本大小。与样本大小的关系是:
Rw 50~99
#- 140-199
中华人民共和国化学工业部1989-03-10批准710-15
r=1518
1990-01-01实施
5实施步骤
n—1 000
GB 11179—89
r— 1820
7= 35~~40
5.1给出Ho:样本米自某个已知理论分布。5.2将观测值排列为顺序统计量
X+X..*,X.
5.3计算理论分布函数值
(j-1,2.**)
5.4按式(2)计算品:
f(x,)dx
22iInF(X) +
1-2j-1
In(—F(X,))
(2)
让算时按表1填满数据。表1中的中间结果计算到五位有效数字,最后结果保留三位有效数字。将表1第10列累加起来,按公式(2)计算得到需。5.5在附录A中与相应的分布函数值(@)。5.6取显著性水平在=0.2。
5.7作出判断:
如果Q()≥1,则拒绝H即拒绝经验分布与理论分布相符合的假设如果()<1一,则接受这种假设。
按o检验正态分布的举例见附录B;BASIC程序见附录C。2
GB1117989
( (-t)+
cexa-tia
)+ex)u
(6)+()
(ca-(e-t)
(x)-(-t)
Eex)&-utkxd-i
GB 11179~89
附录A
G(磁)值
(补充件)
0. 09
GH11179
续表A1
附录B
(参考件)
选用天然橡胶硫化胶试样,按GB528的4号裁刀得到一个&=57的拉伸强度(单位:MPa)的样本。用员方法检验总体是否服从正态分布。B1给出I:样本来自止态分布,
B2将观测值排列为顺序统计量(见表B1)。B3按观测数据计算正态分布的参数估计量X,8和所有的理论分布函数值:肉
S--1. 1237
(j-1,2,-,57)
分别把顺序统计量序号;和顺序统计量X,的理论分布值F(X)填入表1的第1列和第3列,再按表1的第2列及第4至10列各计算式计算,填入对应结果构成表32,其中的第10列数值相加得—28.715.
— 57 — 2 × (- 28. 715)
B4给出显著性水平a-0.2
B5套附录A得Q(o%)-G(0.13)=D.1771—= 0. 8
G(1一
接受所。:原样本来自正态分布的总体。5
.0. 044
0·482
0. 002 99
0. 006 53
0. 020 81
e. (55 61
表 B1
GB 11179—89
排成顺序统计量的原始数据
用表 B1 的数据按表 1 中各计算式计算所得结果5
5. 811 99
--5. 030'87
—3.872 46
—0.050 98
:0.169 84
-2, 889 44 0. 177 42
—2. 713 39
0. 956 11
0. 938 60
—0.214-22
—2. 225 36
- 0. 214 73
0. 125 45
--.2. 075 840, 236 72
0. 165 94
0. 189 05
0. 214 04
0.903 -51
1. 796 11 -0. 236 33
:-1. 665 74
-0.248 40
--1. 541 59
—0. 256 93
0. 833 33
0. 997 01
0. 993 47
0. 933 69
0. 891 97
0. 874 55
心.810 95
—0.003 00
—0.00297
—0. 006 38
0.053 95.
—0. 138 77
— 0. 020 10 : —0. 189 95
0. 021 03
0. 057 210. 053 700. 231 12
0. 068 61 - 0. 063 20 — 0. 277 41 0. 114 32
- 0. 103 29
—0. 318 02
0. 134 050. 118 76
—0.35548
-0. 181 46
0. 157 58
—0.39391
0. 209 55
-0.178 30
0. 785 96
5 -0. 200 710. 457 64
0. 240 851. 423 57 0. 262 240. 816 79 0. 759 150.240 85
0. 269 40
0. 269 40
1. 423 57-0. 287 21
1. 423 57 0. 312 19
1. 311 57 0. 310 64
1. 311 57 0. 333 65
1. 311 57 -- 0. 356 66
1. 311 57 :0. 379 67
0. 745 61
0. 331 13 m 1. 105 25 0. 339 330.363 96
1. 010 700. 328 03
~1. 010 70-0. 345 77
0. 363 96
0. 432 49
0. 432 49
0. 467 67
0. 467 67
0. 467 67
1.010 70-0.363 50
—1. 010 70 :0. 381 23
. 0. 330 87
0. 838 200. 345 57
- 0. 838 200. 360 28
—0. 759 99
0. 759 99
—0.75999
—0. 339 99
—0.353 33
—0. 366 66
0. 675 44
0. 640 35.
0. 622 81
0. 605 26
0. 587 72.
0. 552 63
0. 759 15
.0.730 60
0. 668 87
0. 636 04
0. 636 04
0. 567 51
0. 567 51
:0.532 33
0:53233
—0.275560.224 80.-0.487-04
- 0. 275 56
..- 0. 219 96
—0. 507 18
-0. 275 56 —0. 215 13
0. 319 88-- 0. 239 54
-0.550 18
: 0. 234 04
—0.228 53
-0. 313 880. 223 02
-0.567 68
-- 0. 602 69
— 0. 402 16 -- 0. 278 69
- 0.618 02
.*0. 452 50--0. 305 64
0. 452 50 0. 297 70
:-0. 452 500.289 76
0. 452 50— 0. 281 82
0. 566 50 0. 342 88
0. 566 50-- 0. 332 94
0. 633 67
0. 643 46
—0.65326
0. 663 05
—0. 673 75
0. 678 51
0. 566 50: 0. 323 00
D. 630 50 0. 348 43
— 0. 337 37
-- 0. 326 31
—0. 688 43
一心.69心70
0. 692 97
0. 503 11
0. 573 64
0. 573 64
0: 641 88
0. 674 51
0. 674 51
0. 815 14
0. 815 14
0: 815 14
0. 815 14
0. 837 91
0. 837 91
GB 11179-: 89
续表 B2
— 0. 686 94
—0.343 17
— 0. 618 92
-0. 618 92
— 0. 618 92
0. 500 00
-0. 320 32
—0.33118
0. 342 04
—0.55576
-0. 316 88
0. 443 36 0. 268 35
0. 393 770. 245 24
- 0. 393 770. 252 15
— 0. 259 06
-0. 393 77
—0.23529
—0. 348 31
0. 306 89
— 0.212 67
0. 269 22
— 0. 191 29
0. 235 12
—0,20440
0. 152 40
0. 204 40-0. 155 99
0. 204 40 --0. 159 57
—0.16316
- 0. 176 B4 - 0. 141 26
-0. 176 ±4 -0.147 37
— 0. 152 25
—0. 129 54
-- 0. 152 25 0, 132 21
0. 447 37
0. 359 65
0. 342 11
0. 324 56
0. 289 47
.0. t84 21
0. 149 12
0. 131 58
-- U. 152 250. 134 89
0. 858 78
—0. 137 56
0. 152 25
-0.130 41
0. 120 11
0. 894 81 : -0. 111 11
— 0. 104 29
U. 955 18
0. 962 97
-0. 045 86
-- 0. 037 74:
0. 096 49
0. 078 95
0. 061 40
注:对正态分布检验,除用本方法外,亦可采用GB4882。7
0. 496 89
0. 461 48
0. 461 48
0. 358 12
0. 326 49
心.32549
:0. 294 14
0. 184 86
0. 184 86
0. 184 85
0. 162 09
0. 141 22
0. 141 22
0. 1-41 22
0. 122 26
0. 044 82
(0. 037 03
附录C
\检验的BASIC程序
(参考件)
- 0. 699 39
— 0. 349 70
0.773 330. 373 10
0. 773 33
—0.359 53
—0. 773 33
0. 345 96
0. 852. 46 -0. 366 41
-0.852 46
-0.351 45
-1. 026 88 0. 405 35
0. 603 17
-- 0. 690 71
0. 688 00
0. 683 29
0. 678 09
1. 122 42-0. 423 37
0.668 61
1.122 42 0, 403 68 0, 655 831. 122 420. 383 99
—1. 223 69—0. 397 16
1. 330 79 0. 408 57
- 0. 621 25
— 0. 417 95
1. 443·83
1. 562 92 -0. 425 01
1, 688 16 0. 429 41
—-0.596 19
1. 688 16 . - 0. 399 83
—0. 555 8 1
1, 688 16..0. $70 21
..0. 529 78
—1. 688 16 -0. 340 59
—0.503 75
1. 819 62 --0. 335 19 —0, 479 46-1. 819 62 - 0. 303 27 - 0. 450 64-1. 957 41
-0. 291 89
-- 0. 421 44
1. 957 41 0. 267 55 ~ 0. 389 771. 957 41 0. 223 21 ( 0. 358 10 1. 957 41
0. 188 87
—0. 165 92
—0.32643
—0. 286 03
—0.212.59
- 0. 136 19 -- 0. 180 03
—3.105 06
—3. 105 06
0. 081 :71
0. 126 36
0. 066 32
本程序用方法检验样本的正态分布与双重指数分布,1480~1490语句是留作添写其他分布计7
GB 1117989
算语句的位置。此外,本程序以人机对话式输入分组后给出直方图。源始数据是以TXT为后缴的顺序文件给出的。附录人中的待查数据也是一个数据文件,并命名为A,DA。程序能自动查出对应的表值,当所查数据超出表中的范画时,程序可自动算出该值并打印出米,10 WJDTH LPRINT 132
20 CLS:PRINT TAB(20)
30 PRINTTAB(20)
40 PRINT
“数据分布类型检验总菜单”
50PRINTTAB(5)“1.输入原始数据\,:PRINTTAB(46)“2.构成顺序统计量”60PRINTTAB(5)*3.打印直方图”;70PRTNTTAB(46)“4.2检验\,:PRINTTAB(5)80 PRINT\.PRINT
90INPUT“请选择编号执行对应操作”,BH100ONBHGOSUB120,250,310,710,1600110 GOTO 20
“6.结束”
“输入数据个数”,K:INPUT“输入 TXT 文件名”,Q$120 CLS.INPUT
130 DIM X(K),A(K,11).:OPEN \C.\+Q $ +\.TXT FOR INPUT AS I140FORI=1TOK:INPLT41,X(I).NEXTI.CLOSE#1150 XBA=0:SIGMA=0
160 FOR I=1 TO K
170 XBA=XBA+X(1)
180 NEXT1
190XBA-XBA/K
200 FOR1--1TOK
210SIGMA=SIGMA+(X(I)-XBA)*(X(1)-XBA)220 NFXTI
230 SIGMA=SQR(SIGMA/(K-1))
240 RETURN
250CLS,PRINT“正在排序”
260FORKK=1TOK-1
270 FOR NN=I TO K-1
280 IF X(NN)) X(NN+1) THEN SWAP X(NN),X(NN + 1)290 NEXT NN,KK
300 RETURN
310 CLS:INPUT
320 NH-1000
“输入分组个数\,R:H#一(X(K)一X(1))/R330 IF QI$=\Y\
OR BH=3 THEN ERASE S,ZZ
340 DIM S(R),ZZ(R)
350 FOR RR -1 TO R
360 S(RR)=0
370 ZZ(RR)-X(1)+(RR-0. 5) *H *380 NEXT RR
390 FOR KK-1 TO K
400 FOR RR=1 TO R
GB 11179-- 89
410 F X(KK)<--X(1)+RR *H#+0. 001 AND X(KK)) =X(1)+(RR-1) *H# 0. 001THFN 420 ELSE 440
420 S(RR)-S(RR)-+ 1
430 GOrO 450
410 NEXT RR
450 MEXT KK
460 F-s(1)
470 FORRR-1TOR
480IFS(RR))=FTHEN49DELSF510
490 F=S(RR)
500 R1--RR
610 NEXT RR
520 M0=X(1)(R1-1)*H# +H# * (S(R1)-S(R1-1))/(2+S(RI)-S(R1-1)—S(R1+1))530MZ=X(1)+(R—0.5)*H#
540 MZZ=2. 5/(MZ-M0)
550 FOR RR=1 TO R
“####.###\,X(I)+(RR—1)*H#;.PRINT.560PRINTUSING
“####.###\,X(I1)+RR*H#:PRINT USING“###\,USING
)0THEN580ELSEPRINTUSING“#########”,ZZ(RR):GOTO570 IF S(RR)<
580 PRINT USING *# ## ##. ####\;ZZ(RR);590 FOR NN=1 TO S(RR)
600 PRINT TAB(40+2* (NN.--1)) \\670 IF NN-S(RR) THEN PRINT \620 NEXT NN
630 NEXT RR
640INPUT“打印这幅直方图吗?Y/N”,Q3$650 IF Q3 $ -\y\ THEN Q3$ -\y\660IFQ3$-“Y\THENGOSUB1500
670INPUT‘重新分组吗?Y/N,Q1$680 IF Q1 $=\y\ THEN Q1 S -\Y\690 IF Q1 $ -*Yn THEN 310
700 Q1$--“Y\.RETURN
710 CLS
720PRINT\使用 \法检验橡胶物理试验数据的分布类型是普遍有效的,这里仅给出止态分布与双重指数分布检验,并在1380--1400处留有检验其它分布类型的接口”730 PRINT*
740 PRINT“1 正态分布”
750PRINT“2双重指数分布”
760FRINT“3其它分布\
770PRINT“4检验结束”
780PRINT“\,INPUT\请按序号选择”,BH2790 F BH2=4 THEN 1600
800FOR1-1TOK
GB 1117989
810 A(1,1)=-I:A(T,2)=(2*1-1)/(2*K)820 0N BH2 G0SUB 1350,1450,1480,1600830 A(T,3)=A1:A(I,4)-L0G(A(1,3)):A(1,5)=A(I,2)*A(I,4),A(I,6)=IA(I,2)840 A(I,7)-1—A(I,3):A(I,8)-L0G(A(1,7)):A(I,9)-A(I,6) A(I,8):A(1,10)=A(I,5)+A(I,9):A(I,1)-X(0)
850 NEXT 1
860 SUM-Dwww.bzxz.net
870FOMM-1TOK
880SUM=SUM+A(M,10)
890 NEXT M
900OMEGA=INT((-K2*SUM+0.005)*100/100!910 FOR I-1 TO K
920PRINTUSING“###”,A(1,1);:PRINTUSING“##.###\;A(I,2);930 PRINT USING“##. #####\;A(I,3),+PRINT USING *###.#####\,A(I,4);940 FRINT USING “###.#####\;A(I,5);:PRINT USING *##.#####\,A(I,5);950 PRINT USING *###、####*,A(I,?);:PRINT USING *###. #####\A(I,8)
960PRINTUSING“###.#####”;A(I,9):PRINTUSING“###,#####”A(1,10) ;
970 NEXT I
980LPRINT“?一”LPRINTUSING“###、##”OMEGA990 CODE% = 100+DMEGA
1000 IF CODE%)295 THEN 1010 ELSE 12601010 SS=0
1020 FOR JJ=0 TO 6
1030 IF JI=D THEN A1-1;GOTO 11301040FJJ=ITHENAI-0.5:GOTO11301050 FZ-JJ-0.5
1060 FM-JJ
1070 A1=F7./FM
1080FORI-JJTHEN2STEP-1
1090 FZ-FZ—1
1100 FM--FM-1
1110 A1=A1+FZ/FM
1120 NEXT 11
1130B1=(—1)^JJ*(4*JJ+1)*EXP((—9.87202324#*(4*JJ+1)/(8*OMEGA)))1140 IF ABS(B1) <1E-D9 THEN 1310I150 DBF FNPL(Y)--EXP(OMEGA/(8 * (Y * Y+1))-*OMEGA))
1160 N=1000
1170 H-500/N
1180 S0. 5 * (FNPL(0)—FNPL(1000))10
-((4 * JJ+1) * 3. 1415926# * Y) ~ 2/(81190FORL=1TON
GB 11179--89
1200 S=$+2*FNPL((2*L—1) *H)+FNPL(2*L* H)1210 NEXT I,
1220 CI=1000 *S* 2. 506628/(3 *N* 0MEGA)1230SSSS+AI*BiC1
1240 NEXT JJ
1250 GOTO1310
1260 OPEN“A;DA\AS 2 LEM=241270TIELD#2,8ASN$.8ASA$
1280 GEI #2,CODE%
1290 SS=VaL(A$)
1300 CLOSE
I3I0 LPRINT \Gα?)=\, :LPRINT USING “#, ###\,SS1320INPUT“还作检验吗?Y/N”,Q2$ 1330 F Q2$ -*y\ Then Q2$ --\y\1340 IF Q2 $ -\Y\ THEN. 710 FISE RETURN1350 B=(X(I)—XBA)/SIGMA
1360 C-—6
1370 NI=50
.1380H--(B-C)/(2*NI)
1390 S=0.5* (EXP(—C*2/2))(EXP(—B~2/2))/2.5066282#1400 FOR L- 1 TO NI
: 1410 S=S + 2 *EXP(-(C+(2*L-1) * H) ~ 2/2)/2. 5066282# +EXP(-(C+2 * L *H) 2/2)/2.5066282#
1420 NEXT L
1430 A1=(B—C)*S/(3*N1)
1440RETURN
1450B=
-EXP(MZZ8(X(I)-M0))
1460 A1=I--EXP(B) : IH A11 THEN AI -- 0. 999991470 RETURN
1480REMA1一待检验的某种分布的概率值1490 REMRETURN
1500 FORRR-1TOR
1510 LPRINTUSING“####.##±\,X(1)+(RR-1)*H#:.LPRINT“####.###\,X(1)+RR*H#;:LPRINT USING“###”LPRINT USING
1520 IF S(RR) < >0 THEN 153D ELSE LPRINT USING “# ####.####*;ZZ(RR).GOTO1580
1S30LPRINTSING“####,####”ZZ(RR)
1540 FOR NN=1 TO S(RR)
1550 LPRINT TAB(40+ 2 * (NN-1));\\1560IFNN-S(RR)THENI.PRINT
1570 NEXT NN
1580 NEXT RR
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。