本标准适用于对抽自正态总体的随机样本所作的一系列试验的基础上，在总体方差未知的情况下，估计该总体的均值；或者利用试验所得的数据计算出一个区间，使得这个区间以给定的概率包含总体均值。对于总体概率部分遵从正态分布的假定可以广泛地得到满足：在一定的试验条件下，所得试验结果的分布经常是正态分布或者近似正态分布。本标准假定，用来进行测定的个体，构成一个来自原总体的独立随机样本。 GB 3360-1982 数据的统计处理和解释 均值的估计和置信区间 GB3360-1982 标准下载解压密码：www.bzxz.net
本标准适用于对抽自正态总体的随机样本所作的一系列试验的基础上，在总体方差未知的情况下，估计该总体的均值；或者利用试验所得的数据计算出一个区间，使得这个区间以给定的概率包含总体均值。对于总体概率部分遵从正态分布的假定可以广泛地得到满足：在一定的试验条件下，所得试验结果的分布经常是正态分布或者近似正态分布。本标准假定，用来进行测定的个体，构成一个来自原总体的独立随机样本。

中华人民共和国国家标准
数据的统计处理和解释
均值的估计和置信区间
Statistical interpretation of dataEstimation of the mean-Confidence intervalUDC519.25:620
GB 3360--82
本标准适用于对抽自正态总体的随机样本所作的一系列试验的基础上，在总体方差未知的情形下，估计该总体的均值，或者利用试验所得的数据计算出一个区间，使得这个区间以给定的概率包含总体均值。对于总体概率分布遵从正态分布的假定可以广泛地得到满足：在一定的试验条件下，所得试验结果的分布经常是正态分布或者近似正态分布。本标准假定，用来进行测定的个体，构成个来自原总体的独立随机样本。
变换试验结果的原点或单位可以使计算简化。如果没有试验上，技术或其他的明显理由作为依据，则不许剔除任何观测值或修正可疑的观测值。试验方法可能受到系统误差（可确定原因的误差）的约束。本标准假定没有系统误差。系统误差的存在可能使下述的方法失效。计算所得的区间称为均值的置信区间，与它相关联的是置信水平。置信水平是置信区间包含总体均值的概率，通常用百分数表示。本标准仅考虑95%和99%两个水平。本标准是参考国际标准ISO2602《试验结果的统计解释一均值的估计和置信区间》（1980年第二版）制订的。
1均值的估计
1.1不分组的情形
在剔除可疑数据后，这批数据包含n个观测值；（i=1,2，，n），其中某些可能取相同的值。用n个数据的算术平均x估计正态分布的均值μX-Ir
1.2分组的情形
当数据的个数很大（比如在50以上）时，可以将它们按等间隔分组。在某些情形，也可能直接获得分组的数据。
n；表示第i组的频数，即是第i组中数据的个数。k表示组数，则有
表示第i组的中点，用所有组的中点的加权算术平均>作为均值u的估计。k
国家标准局1982-12-30发布
1984-01-01实施
2均值的置信区间
GB3360—82
利用总体均值和标准差的估计量可以计算总体均值的置信区间。计算置信区间的另一种方法是利用极差，这种方法在附录A中给出。2.1标准差的估计
2.1.1不分组的情形
标准差α的估计公式如下：
式中：αi-
n-l台
第i个观测值（i=1.2，，n），
观测值的总个数，
一n个观测值的算术平均。
为了计算方便，建议使用下列公式S=.
2.1.2分组的情形
标准差?的估计公式如下：
为了计算方便，建议使用下列公式S=
式中：—
Zn (yi -j)2
n-1-=1
第i组的中点（i=1,2，，k）
组数：
ni—第i组中观测值的个数
-观测值的总个数，n=≥ni
又—各组中值的加权算术平均。2.2均值的置信区间
对于所选取的置信水平（95%或99%），根据特定情形，确定双侧的或单侧的置信区间。2.2.1双侧置信区间
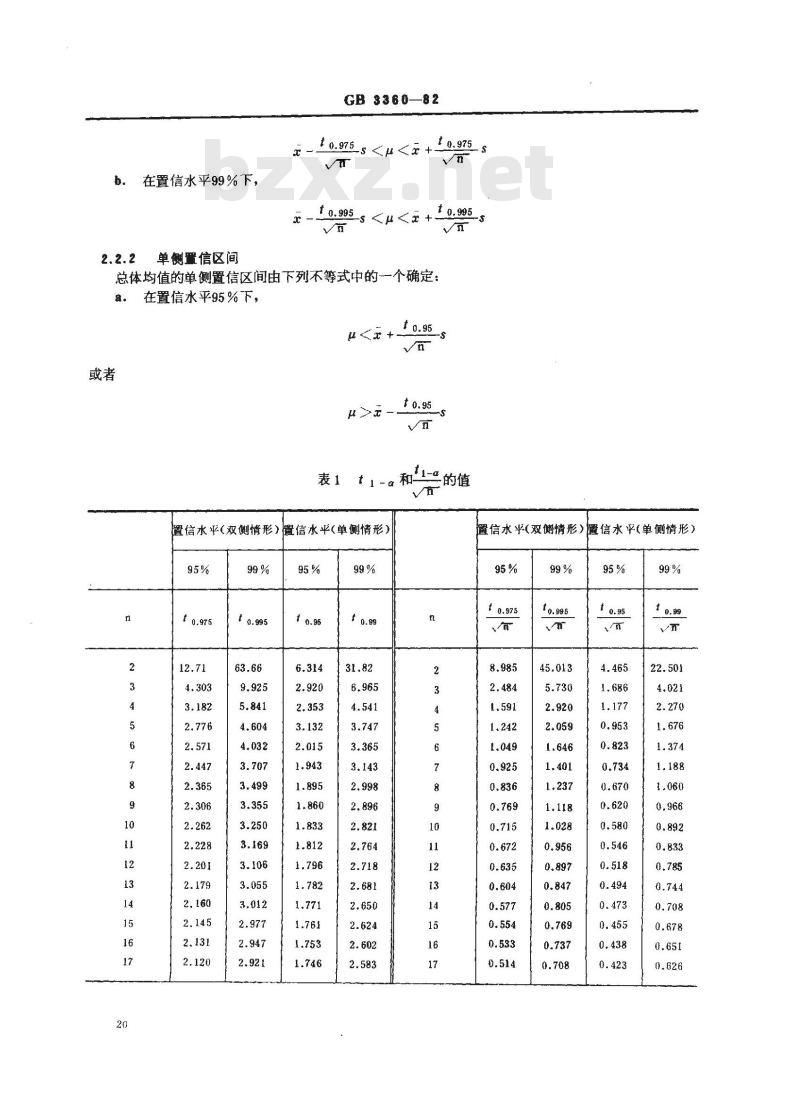
总体均值的双侧置信区间由下列的双重不等式确定：a.
在置信水平95%下，
b。在置信水平99%下，
单侧置信区间
GB 3360—82
t o.975 s
± 0. 975-s <μ<5 +
t 0.995-s <μ< +
总体均值的单侧置信区间由下列不等式中的-一个确定：在置信水平95%下，
1-的值
表1t，
1-g和
置信水平(双侧情形)置信水平(单侧情形）95%
置信水平（双侧情形）
信水平(单侧情形）
GB 3360--82
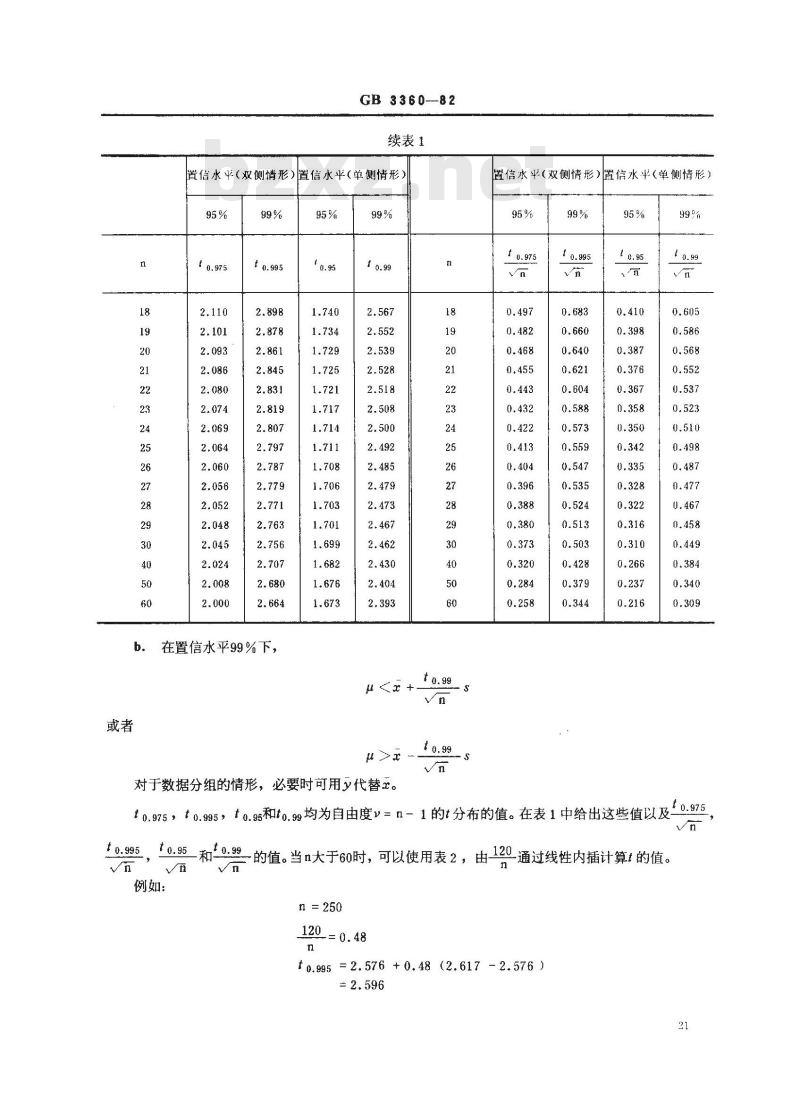
续表1
置信水平(双侧情形）置信水平(单侧情形）95%
在置信水平99%下，
对于数据分组的情形，必要时可用代替。to.99
置信水平(双侧情形)置信水平(单侧情形）95%
t0.975，t0.995，t0.95和to.99均为自由度v=n1的t分布的值。在表1中给出这些值以及Vn
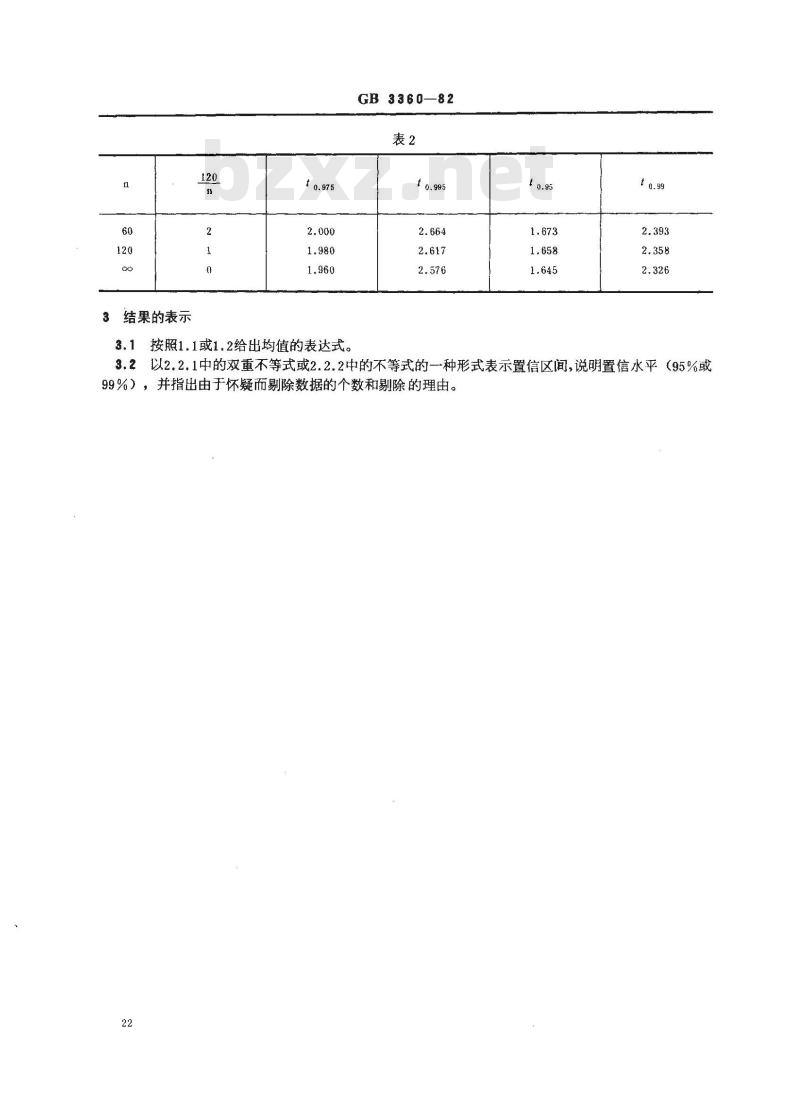
，10.95和“09—的值。当n大于60时，可以使用表2，由120-通to.995.
-通过线性内插计算t的值。
例如：
n = 250
t o.995 = 2. 576
3+0.48（2.617此内容来自标准下载网
—2.576)
结果的表示
3.1按照1.1或1.2给出均值的表达式。GB336082
以2.2.1中的双重不等式或2.2.2中的不等式的一种形式表示置信区间，说明置信水平（95%或99%），并指出由于怀疑而剔除数据的个数和剔除的理由。22
GB 3360--82
附录A
用极差确定均值的置信区间
（补充件）
如果将观测值从小到大排列，即2n，则R=被定义为样本极差。仍然假定总体是正态分布。当观测值的个数较少时，比如说小于或等于12，可以利用样本极差来确定总体均值的置信区间。这种算法优点是比较快，缺点是通常导出一个较宽的置信区间，而且对观测值偏离正态假设比较敏感。
双侧置信区间，
总体均值的双侧置信区间由下列双重不等式确定：在置信水平95%下
- q0. 975 R<μ< + q0.975 R
在置信水平99%下
单侧置信区间
-q0.995 R总体均值的单侧置信区间由下列不等式中的一个确定：a，在置信水平95%下
在置信水平99%下
或者，μ>q0.95R
μ<+q0.9g R
或者，μ>q0.9gR
系数90.975，90.995，90.95，90.99在附表中给出。附表
置信水平 (双侧情形)
附加说明：
本标准由电子工业部标准化研究所提出。置信水平 (单侧情形)
本标准由电子工业部标准化研究所、科学院系统科学研究所、哈尔滨工业大学起草。23
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。