GB 4086.3-1983
基本信息
标准号: GB 4086.3-1983
中文名称:统计分布数值表 t分布
标准类别:国家标准(GB)
英文名称:Tables for statistical distributions;t-distribution
标准状态:现行
发布日期:1983-12-21
实施日期:1984-10-01
出版语种:简体中文
下载格式:.rar.pdf
下载大小:625510

标准分类号
标准ICS号:数学、自然科学>>07.020数学
中标分类号:综合>>基础学科>>A41数学
关联标准
出版信息
出版社:中国标准出版社
页数:16页
标准价格:18.0 元
出版日期:1984-10-01
相关单位信息
首发日期:1983-12-21
复审日期:2004-10-14
起草人:杨自强
起草单位:全国统计方法应用标技委
发布部门:国家标准化管理委员会
主管部门:国家标准化管理委员会
标准简介
本标准包括统计学中常用的t分布的两种数值表。 GB 4086.3-1983 统计分布数值表 t分布 GB4086.3-1983 标准下载解压密码:www.bzxz.net
本标准包括统计学中常用的t分布的两种数值表。
本标准包括统计学中常用的t分布的两种数值表。
标准图片预览

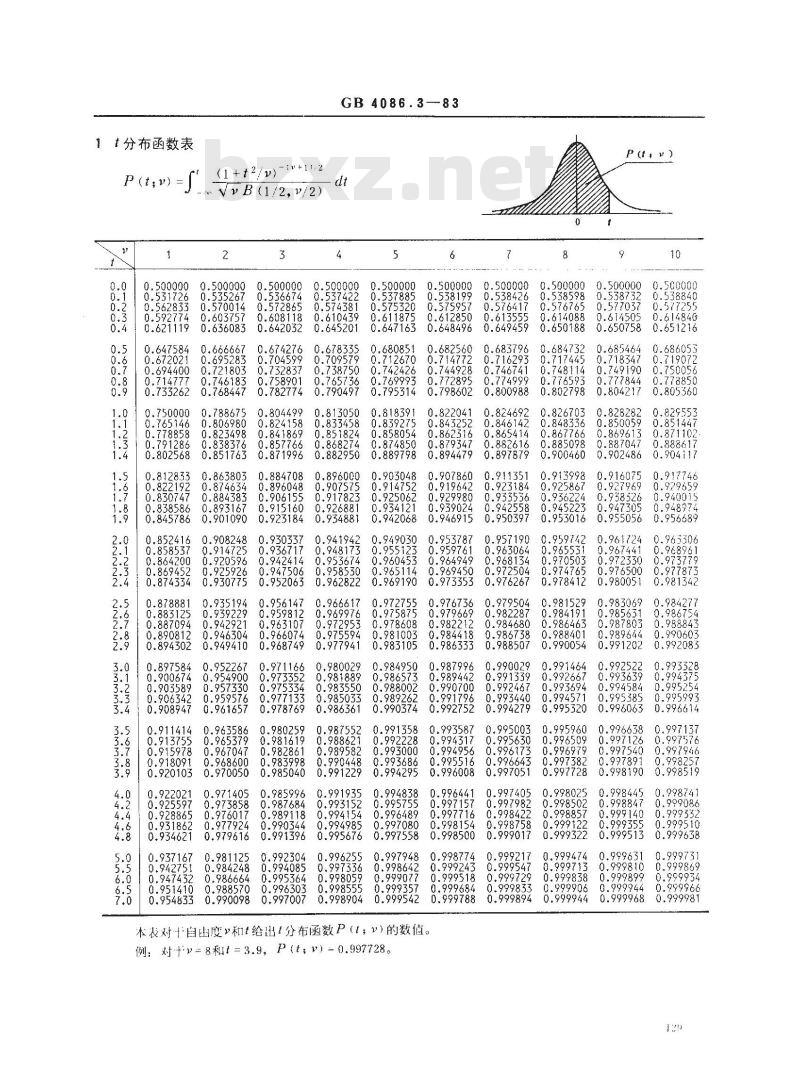

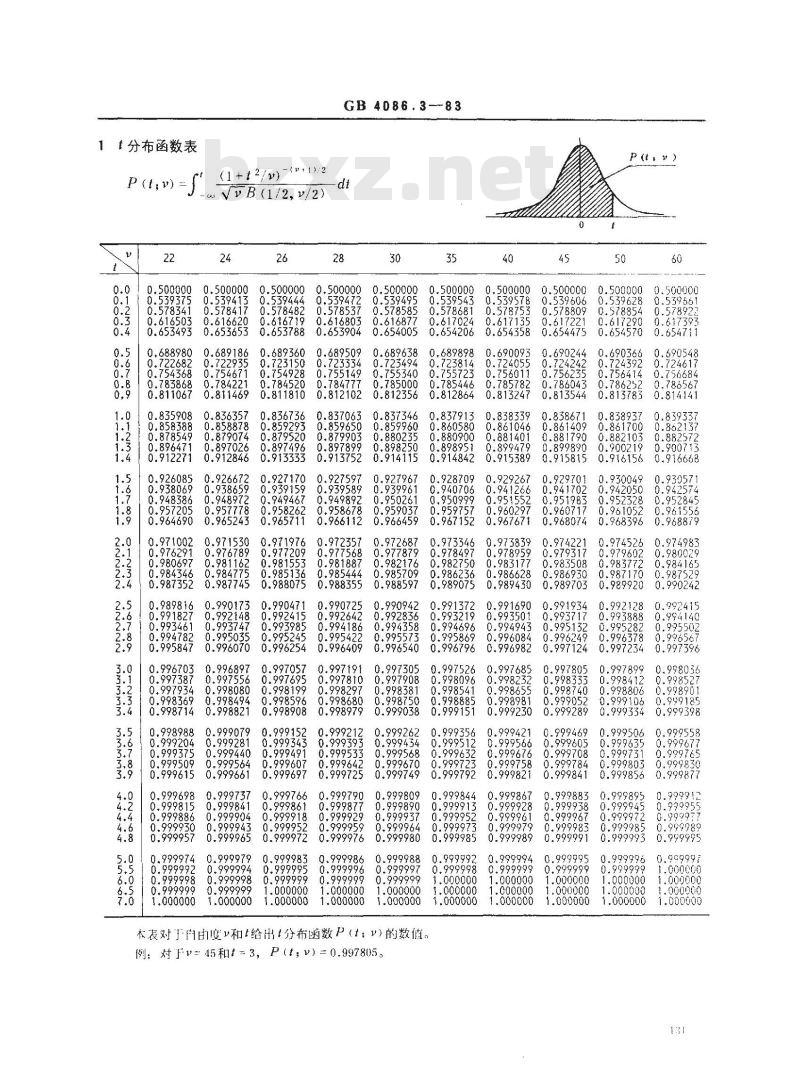

标准内容
中华人民共和国国家标准
统计分布数值表
t分布
Tables for statistical distributionst-distribution
UDC 311.13(083.5)
GB 4086.3--83
本标准包括统计学中常用的分布的两种数值表,它们的名称、表距和精度如下:1分布函数表
t分布分位数表
=1(1)20(2)30(5)50,60
t =0(0.1)4(0.2)5(0.5)7
b= 0.5(0.05)0.95.0.975. 0.98.0.99. 0.995.0.9975, 0.998, 0.999, 0.9995, 0.9998,0.9999V=1(1)30(2)40(5)70(10)120150,180,240,cx表中的分位数对应于下侧概率。虽然表中给出5~6位小数,但是在使用中需要取几位,要由实际问题决定。在应用中不能满要求时,可参考附录的处理方法。国家标准局1983-12-21发布
6位小数
5位小数
19841001实施
838586
858537
864200
.89081
.897584
900674
.931862
951410
746183
788675
863803
908248
920596
925926
930775
984248
986664
988570
.824158
.857766
871996
.884708
936717
.942414
981619
983998
987684
290344
992304
994085
8:996303
868274
969976
981889
990448
.996255
.903048
.97587
8:999542
959761
994317
表对自出度和t给出分布函数P()的数值。例:对于v=8和t=3.9,P(t;V)=0.997728。0.774999
992467
965531
998857
999838
999906
887047
902486
8:994584
.996638
.998847
999140
999355
999810
940015
948974
956689
977873
990603
.993328
995993
997137
999332
999638
337333
719668
.919121
941402
950342
989672
.997515
998249
577585
615345
.720167
8:951484
965672
975932
979901
988387
.991978
996830
999567
539065
577712
615540
8:972094
8:988997
997126
639119
892701
998551
.99902
721269
893388
909072
973472
981888
987747
998021
998388
999289
999742
753010
968614
990330
996560
997740
8:999214
999363
本表对于自度和给出t分布涵数P(t;)的数值。P(t; w)=#.752302
例:对14和t=0.7,
753302
834334
979038
8:998668
:997376
997885
998628
998896
999111
999285
299699
100001
999945
578139
894999
8:936498
946827
.539304
578797
1989130
997052
1997643
998802
999240
999395
999580
999731
999827
999889
999954
.999984
999996
817919
895808
998212
8:999291
999551
.999648
999780
999913
999949
999966
999988
t分布函数表
p(t,v) =
539375
688980
.722682
835908
926085
964690
0:980697
989816
991877
994782
996703
997387
.998988
.999375
.999509
999698
1999815
(1++2/v) -(v+1)/2
-αVVB(1/2, v/2)
539413
.836357
.957778bzxz.net
.976789
987745
992148
285035
998080
999564
539444
616719
836736
879520
981553
990471
995245
.997057
1998199
.998596
.999766
8999952
GB 4086.3--83
500000
723334
755149
8:939589
.977568
981887
.998297
998680
.999790
.500000
539495
723494
755340
.988597
990942
0994358
578681
654206
689898
723814
0994696
.99984
木表对于自由度v和t给出t分布函数P(t;\)的数值。例:对Fv=45和t=3,P(t;v)=0.997805。40
500000
724242
998740
999052
999883
999983
000000
539628
724392
756414
.996378
.998806
999895
999972
8:756684
.882572
.939571
942574
.961556
.974983
980029
990242
992415
994140
996567
997396
998901
:999185
999677
8:999765
999912
(分布分位数表
tp(v):f
狂530
8:80000
(1 +t2/v)\(#+*) 2
VUR(1/2, V/2)
0:0008
e:0008
8:1233
.26317
8:25692
.25658
:25419
GB4086.3-83
8:3396
8:38997
138978
.54348
.54153
133144
8·52967
:88485
.67801
本表对于自出度\和下侧概率给出1分布的分位数(V)例:对=100和-0.90,()=1.29007。当p0.5时,tp() t-p()。例:ta.t(100)与双侧概率(相应的分位数为:α?(:132
.90570
th.u(100)=-1.29007
:18957
111916
1:07928
.05932
.05752
t。(v)
.47588
.39682
.34503
.34061
.32124
.31143
.30695
129582
.29103
.28509
.91999
.94318
对 +m- 100利a- 0.2, t: α2 (v)- (3u(100) -1.29007.分布分位数表
tp(u):
10:7:8:01
.30265
(1+t2/)(#+1)/2
wB(1/2,/2)
.20099
.06390
.05954
.92439
2:00030
.99444
1:9996
.98667
120470
.09936
.09578
.08088
.07631
:50832
:4998
GB4086.3-83
2:67729
.90602
.80703
318.30884
.06433
:81778
本表对于自由度和下侧概率p给出t分布的分位数t(v)。例:对于y=20和p=0.999,tp()=3.55181。4.
.43698
3:45019
.22041
当p0.5时,tp(v)- tr-p(v)。例:to.ol(20)-- to.9gy(20)=-3.55181。.01500
.29053
159794
3183.0988
79-7000
.67757
2:81839
3:88218
与双侧概率α相应的分位数为t::a/2(V)。例:对于=20和α0.002,t1-a/z()-to.99g(20)=3.5518113.
GB4086.3-83
附录A
计算方法
(参考件)
这里给出本标准两种数值表的计算方法。在本标准所列数表不能满足要求时,可参考这些算法及附录B的程序进行计算,或者使用插值方法作粗略计算。A.1t分布的定义与记号
自由度为的t分布的密度函数是
f(t;v)=
式中: B(a,b)=
分布函数是
B(,)
=1,2,3,。
l a-1(1-)b-1d。
P(t, v)
与下侧概率p对应的分位数tp()满足如下方程:(1+
f (t,v) dt.
P(tp(v),v)= p。
注:t分布在自由度v→α时的极限分布为正态分布。A.28分布与t分布的关系
A.2.1B分布的定义与记号
参数为α,b的β分布的密度函数是B(d,6)a+(1)--, 0≤<, a>0, b>0.fe(a,a, b)=
分布函数是
-29-1 (1- )b\1d。
Ir(a,b)= {
。B(a,b)
与下侧概率p对应的分位数p(a,b)满足方程rxp(a,b)
A.2.2β分布与t分布的关系
B(a,b)
对比t分布与β分布得t分布的分布函数P(t;v)=1
武中: 3
a-l(1-α)b-Id=p。
Ir(a,b),
分位数是
式中:
l 2(1 - p)
A.3计算方法
GB4086.3—83
tp(v)= sign(p-
A.3.1其它分布的引用
p* (a, b)
a.根据上述,t分布计算可转化为β分布计算。因此这里实际上是给出β分布的计算方法。b。本附录涉及正态分布分位数up的计算,可参考GB4086.1-83《统计分布数值表正态分布》的附录A。
A.3.2B分布密度函数与分布函数的计算使用由分部积分法得到的递推公式I(a+1,b)= Is(a,b)-1Ur(a,b),
IUr(a,b),
I, (a, 6+1)= I(a, b)+-
Us (a+1,b)=Us(a,b) α+b
tU (a,b+1)=U+(a,b)-+tb
(1-α)。
式中:U(a,b)=
-α\(1-α)b
这里只考虑α与b都是整数倍的情形,这时递推初值为【1()
)={-
I(,)=,
I(1,)=V-,
I(1,1)=α,
U(,)=(1-),
U( )(),
U(1,)=
lUr(,1)=α(1-z)。
A.3.38分布分位数的计算
若参数a,b是一
-或1,由下式直接计算
GB4086.3-83
αp(
1+ tan2(号(1- p)),
1)=2,
p(1,)=1(1-p),
l cp(1,1)= p.
其它场合使用送代法计算(见GB4086.1的附录A.3),初始值由如下方法给出:rp(a,b)=
a。若α,b两参数中有一个等于,于号,则定义
t = tp*+
式中u*是与下侧概率p*对应的正态分位数,p* = -
F=2(当b=
-Yi(up*),
v=26,F=
(当a=
22(u3+u),
(5u5+ 16u3 +3u),
Y2(u)=
Y4(u)=
(3u? +19u5+17u3-15u),
(79u9 +776u? + 1482u5-1920u3- 945u),Ys(u)=
(27ull+339u9+930u?-1782u5-765u3+17955u)。213.32.5
b。若c,6两参数中没有一个等于,则定义F
式中:*=1p,c=
(1-c)(1-d)+up*(ic)2d+(1-d)2c-cdus.(1- d)2- dug*
B.1说明
GB4086.3—83
附录B
计算程序
(参考件)
这单给出用F本标准实际计第的四个FORTRAN语高了程序。它们是BFTAFD:用」计算8分布的密度函数和分布函数,BETAXD:用于计算βB分布的分位数,TFD:用于计算1分布的分布函数,TXD:用F计算t分布的分位数。
程序使用附录A的计算方法,即把t分布转化为β分布计算,因而两个分布的计算程亲是必要的此外,它们运行时又需调用两个F态分布于程序NORFD与NORXD,可参考GB4086.J的附录B:望然本标准印出的数表只取5~6位小数,但程序的计算精度通常叫达10·10程序
SUBROUTINE BETAFD(X,N2A,N2B,P,DENS)INTEGER N2A,N2B
DOUBLE PRECISION X,P,UENS
**PURPOSE**
DISTRIBUTION FUNCTION AND DENSITY OF BETA DISTRIBUTIONWITH HALF INTEGER PARAMETERS** ARGUMENTS **
ONNETRY
ON RETURN
N2A=2*A. (A-1)TH POWER OF X IN BETA DISTRIBUTIONBETF0001
BETF0002
BETF0003
BETF0004
BETF0005
BETF0006
BEIF0007
BETF0008
BETF0009
BETF0010
BETF0011
BETF0012
BETF0013
BETFO014
N2B=2*B. (B-1)TH POWER OF (1-X) IN BETA DISTRIBUTION BETF0015BETF0016
BETA POINT
RE1F0017
LOWER PROBABILITY
DENSITY
**REQUIREDROUTINES **
** ALGORITHM **
THE RECURRENCE FORMULA
I(X,A+1,B) = I(X,A,B) - (U(A.B)/A).ICX.A,B+1) = I(X,A,B) + (U(A,B)/B),U(A+1,B) = U(A.B)*X*(A + B)/A.U(A,B+1) = U(A,B)*(1-X)*(A+B)/B,WHERE
I(X.A,B) IS DISTRIBUTION FUNCTION OF BETA DISTRIBUTION.U(A,B) = X**A*(1-X)**B/BETA(A,B),BETA(A,B) IS BETA FUNCTION.
INITIAL VALUES
I(X,1/2,1/2) = 1 - (2/PAI)*ATAN(SQRI((1-X)/X)),I(X,1/2,1) = SQRI(X).
I(X,1.1/2) = 1 - SQRT(1-X).
I(X,1,1) = X,
BETF0018
BETF0019
BETF0020
BETF0021
BETF0022
REIF0023
BETF0024
BETF0025
BETF0026
BETF0027
BETF0028
BFIF0029
BEIF0030
BETF0031
BETF0032
BI.TF0033
BEIF0034
BETF005S
BETFO036
BE1F0037
BETF0038
GB4086.3--83
U(1/2.1/2)=SQRT(X(1-X))/PAI,U(1/2,1) = SQRt(X)*(1-X)/2.
U(1.1/2) = X+SQRT(1-X)/2,
U<1,1) = X(1-X).
INTEGER M,N
DOUBLEPRECISIONS.FI,FM
S = DSQRT(1.000 - X)
M = 2*(N2B/2) - N2B + 2
N = 2*(N2A/2) - N2A + 2
INITIAL VALUE
IF《M.EQ. 2)GOTO 20
IF (N .EQ. 2) G0 T0 10
N2AISODDANDN2BISODD
P = 1.0D0 - 0.63661977236758134D0*DAIAN(S/DSQRT(X))DENS=0.31830988618379067D0*S*DSQRT(X)GOTO 40
CONTINUE
N2A IS EVEN AND N28 IS 000
P = 1.000 - s
DENS = 0.500*S*X
GD TO 40
CONTINUE
IF (N .EQ. 2) GO TO 30
N2A IS ODD AND N2B IS EVEN
P = DSQRT(X)
DENS = 0.5DO*(1.0DO X)*P
GO TO 40
CONTINUE
N2A IS EVEN ANU N2B IS EVEN
DENS = X*(1.ODO X)
40 CONTINUE
SO CONTINUE
RECURRENCE
DO 60 I = N,N2A,2
IF (N2A .LE. I) GO TO 70
P = P - 2.ODO/FI*DENS
DENS = DENS*X*(FM + FI)/FI
60 CONTINUE
7O CONTINUE
DO 80 I = M.N2B,2
IF (N2B .LE. I) GO TO 90
P = P + 2.0D0/FM*BENS
DENS - DENS*(1.ODO - X)*(FM + FI)/FM80 CONTINUE
90 CONTINUE
DENS = DENS/(X*(1.ODO - X))
RETURN
BETF0039
BETF0040
BETF0041
BETF0042
BETF0Q43
BETF0044
BETF0045
BETF0046
BETF0047
BETF0048
BETF0049
BETF0050
BETF0051
BETF0052
BETF0053
BETF0054
BETF0055
BETF0056
BEIF0057
BETF0058
BETF0059
BETF0060
BETF0061
BETF0062
BETF0063
BETF0Q64
BETF006S
BETF0066
BETF0067
BETF0068
BETF0069
BETF0070
BETF0071
BETF0072
BETF0073
BETF0074
BEIF0075
BETF0076
BETF0077
BETF0078
BETF0079
BETF0080
BETF0081
BETF0082
BETF0083
BETF0084
BETF0085
BETF0086
BETF0087
BETF0088
BETF0089
BETF0090
BETF0091
BETF0092
BETFQ093
BETF0094
BETF0095
BETF0096
BETF0097
BETF0098
BETF0099
BETF0100
GB4086.3—
SUBROUTINE BETAXD(P,N2A.N28,EPS,X,IER)INTEGER N2A,N28,IER
DOUBLE PRECISION P,EPS.X
** PURPOSE **
PERCENTAGE POINT OF BETA DISTRIBUTION (INCOMPLETE BETAFUNCTION RATIO) WITH HALF INTEGER PARAMETERS** ARGUMENTS **
DN NETRY
N2A=2*A, (A-1)TH POWER OF × IN BETA DISTRIBUTIONN2A
ON RETURN
BETX0001
BETX0002
BETX0003
BETX0004
BEIX0005
BETX0006
BETX0007
BETX0008
BEIX0009
BETX0010
BETX0011
BE1X0012
BE1x0013
BETX0014
N2B=2*B, (B-1)TH POWER OF (1-X) IN BETA DISTRIBUTION BETX0015LOWER PROBABILITY
REQUIRED PRECISION
PERCENTAGE POINT
ERROR PARAMETER
IER.NE.0 INDICATES P.LE.O OR P.GE.1** REQUIRED ROUTINES **
BETAFD
PERCENTAGE POINT OF NORMAL DISTRIBUTIONDISTRIBUTION FUNCTION OF NORMAL DISTRIBUTIODISTRIBUTION FUNCTION OF BETA OISTRIBUTION**ALGORITHM **
WHEN N2A AND N2B ARE EQUAL TO 1 OR 2, THE PERCENTAGE POINTX(P,N2A/2.N28/2) IS CALCULATED BY FORMULAX(P,1/2,1/2) = 1/(1 + (TAN((PA1/2)*(1-P)))**2),X(P.1/2,2/2) = P**2,
X(P,2/2,1/2) = 1 - (1-P)**2,X(P,2/2,2/2) = P,
FOR THE OTHER UALUES OF N2A AND N2B,HITOTUMATU-S ITERATIONMETHOD IS USED, INITIAL VALUE IS CALCULATED BY YAMAUTI-SFORMULA AND PAULSON-TAKEUCHI-S FORMULA. SEE Z. YAMAUTI.STATISTICAL TABLES AND FORMULAS WITH COMPUTER APPLICATION,JSA-1972, B(2.10)-P.27, B(2.31)-P.33.INTEGER N,MN
DOUBLE PRECISION PAIS.PP,U.DENS,DDENS,R,RDOT.A.B.C.D.F1.F2DATA PAI5/1.57079632679489662D0/IER=O
IF (P .GT. 0.ODO .AND. P .LT. 1.ODO) GO TO 10IER = 129
IF (P .LE. 0.0D0) X = 0.0D0
IF (P .GE. 1.0D0) X = 1.0DO
GOTO100
1O CONTINUE
IF (N2A .GT、 2 .OR. N2B .GT. 2) GO TO 30CASE N2A=1.2 AND N2B=1,2
IF (N2A .EQ. 1 ,AND. N2B -EQ. 1) X = 1.0D0/(1.0D0 +(DSIN(PAI5*(1.ODO-P))/DCOS(PAI5*(1. ODO-P)))**2)IF (N2A .EQ. 1 .AND. N?B .EQ. 2) X = P**2BETX0016
BETX0017
BETX0018
BETX0019
BETX0020
BEIX0021
BEIX0022
BETX0023
BE1X0024
BETX0025
BETX0026
BETX0027
BETX0028
BETX0029
BETX0030
BETX0031
BETX0032
8E1X0033
BETX0034
BETX0035
BETX0036
BETX0037
BEIX0038
BETX0039
BETX0040
BETX0041
BETX0042
BETX0043
BETX0044
BEiX0045
BETX0046
BETX0047
BETX0048
BETX0049
BETX0050
BETX0051
BETX0052
BEIX0053
BEIX0054
BETX0055
BETX0056
BE1X0057
BEIX0058
BEIXOS9
BETX0060
BETXOCG1
BETX0062
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。
统计分布数值表
t分布
Tables for statistical distributionst-distribution
UDC 311.13(083.5)
GB 4086.3--83
本标准包括统计学中常用的分布的两种数值表,它们的名称、表距和精度如下:1分布函数表
t分布分位数表
=1(1)20(2)30(5)50,60
t =0(0.1)4(0.2)5(0.5)7
b= 0.5(0.05)0.95.0.975. 0.98.0.99. 0.995.0.9975, 0.998, 0.999, 0.9995, 0.9998,0.9999V=1(1)30(2)40(5)70(10)120150,180,240,cx表中的分位数对应于下侧概率。虽然表中给出5~6位小数,但是在使用中需要取几位,要由实际问题决定。在应用中不能满要求时,可参考附录的处理方法。国家标准局1983-12-21发布
6位小数
5位小数
19841001实施
838586
858537
864200
.89081
.897584
900674
.931862
951410
746183
788675
863803
908248
920596
925926
930775
984248
986664
988570
.824158
.857766
871996
.884708
936717
.942414
981619
983998
987684
290344
992304
994085
8:996303
868274
969976
981889
990448
.996255
.903048
.97587
8:999542
959761
994317
表对自出度和t给出分布函数P()的数值。例:对于v=8和t=3.9,P(t;V)=0.997728。0.774999
992467
965531
998857
999838
999906
887047
902486
8:994584
.996638
.998847
999140
999355
999810
940015
948974
956689
977873
990603
.993328
995993
997137
999332
999638
337333
719668
.919121
941402
950342
989672
.997515
998249
577585
615345
.720167
8:951484
965672
975932
979901
988387
.991978
996830
999567
539065
577712
615540
8:972094
8:988997
997126
639119
892701
998551
.99902
721269
893388
909072
973472
981888
987747
998021
998388
999289
999742
753010
968614
990330
996560
997740
8:999214
999363
本表对于自度和给出t分布涵数P(t;)的数值。P(t; w)=#.752302
例:对14和t=0.7,
753302
834334
979038
8:998668
:997376
997885
998628
998896
999111
999285
299699
100001
999945
578139
894999
8:936498
946827
.539304
578797
1989130
997052
1997643
998802
999240
999395
999580
999731
999827
999889
999954
.999984
999996
817919
895808
998212
8:999291
999551
.999648
999780
999913
999949
999966
999988
t分布函数表
p(t,v) =
539375
688980
.722682
835908
926085
964690
0:980697
989816
991877
994782
996703
997387
.998988
.999375
.999509
999698
1999815
(1++2/v) -(v+1)/2
-αVVB(1/2, v/2)
539413
.836357
.957778bzxz.net
.976789
987745
992148
285035
998080
999564
539444
616719
836736
879520
981553
990471
995245
.997057
1998199
.998596
.999766
8999952
GB 4086.3--83
500000
723334
755149
8:939589
.977568
981887
.998297
998680
.999790
.500000
539495
723494
755340
.988597
990942
0994358
578681
654206
689898
723814
0994696
.99984
木表对于自由度v和t给出t分布函数P(t;\)的数值。例:对Fv=45和t=3,P(t;v)=0.997805。40
500000
724242
998740
999052
999883
999983
000000
539628
724392
756414
.996378
.998806
999895
999972
8:756684
.882572
.939571
942574
.961556
.974983
980029
990242
992415
994140
996567
997396
998901
:999185
999677
8:999765
999912
(分布分位数表
tp(v):f
狂530
8:80000
(1 +t2/v)\(#+*) 2
VUR(1/2, V/2)
0:0008
e:0008
8:1233
.26317
8:25692
.25658
:25419
GB4086.3-83
8:3396
8:38997
138978
.54348
.54153
133144
8·52967
:88485
.67801
本表对于自出度\和下侧概率给出1分布的分位数(V)例:对=100和-0.90,()=1.29007。当p0.5时,tp() t-p()。例:ta.t(100)与双侧概率(相应的分位数为:α?(:132
.90570
th.u(100)=-1.29007
:18957
111916
1:07928
.05932
.05752
t。(v)
.47588
.39682
.34503
.34061
.32124
.31143
.30695
129582
.29103
.28509
.91999
.94318
对 +m- 100利a- 0.2, t: α2 (v)- (3u(100) -1.29007.分布分位数表
tp(u):
10:7:8:01
.30265
(1+t2/)(#+1)/2
wB(1/2,/2)
.20099
.06390
.05954
.92439
2:00030
.99444
1:9996
.98667
120470
.09936
.09578
.08088
.07631
:50832
:4998
GB4086.3-83
2:67729
.90602
.80703
318.30884
.06433
:81778
本表对于自由度和下侧概率p给出t分布的分位数t(v)。例:对于y=20和p=0.999,tp()=3.55181。4.
.43698
3:45019
.22041
当p0.5时,tp(v)- tr-p(v)。例:to.ol(20)-- to.9gy(20)=-3.55181。.01500
.29053
159794
3183.0988
79-7000
.67757
2:81839
3:88218
与双侧概率α相应的分位数为t::a/2(V)。例:对于=20和α0.002,t1-a/z()-to.99g(20)=3.5518113.
GB4086.3-83
附录A
计算方法
(参考件)
这里给出本标准两种数值表的计算方法。在本标准所列数表不能满足要求时,可参考这些算法及附录B的程序进行计算,或者使用插值方法作粗略计算。A.1t分布的定义与记号
自由度为的t分布的密度函数是
f(t;v)=
式中: B(a,b)=
分布函数是
B(,)
=1,2,3,。
l a-1(1-)b-1d。
P(t, v)
与下侧概率p对应的分位数tp()满足如下方程:(1+
f (t,v) dt.
P(tp(v),v)= p。
注:t分布在自由度v→α时的极限分布为正态分布。A.28分布与t分布的关系
A.2.1B分布的定义与记号
参数为α,b的β分布的密度函数是B(d,6)a+(1)--, 0≤<, a>0, b>0.fe(a,a, b)=
分布函数是
-29-1 (1- )b\1d。
Ir(a,b)= {
。B(a,b)
与下侧概率p对应的分位数p(a,b)满足方程rxp(a,b)
A.2.2β分布与t分布的关系
B(a,b)
对比t分布与β分布得t分布的分布函数P(t;v)=1
武中: 3
a-l(1-α)b-Id=p。
Ir(a,b),
分位数是
式中:
l 2(1 - p)
A.3计算方法
GB4086.3—83
tp(v)= sign(p-
A.3.1其它分布的引用
p* (a, b)
a.根据上述,t分布计算可转化为β分布计算。因此这里实际上是给出β分布的计算方法。b。本附录涉及正态分布分位数up的计算,可参考GB4086.1-83《统计分布数值表正态分布》的附录A。
A.3.2B分布密度函数与分布函数的计算使用由分部积分法得到的递推公式I(a+1,b)= Is(a,b)-1Ur(a,b),
IUr(a,b),
I, (a, 6+1)= I(a, b)+-
Us (a+1,b)=Us(a,b) α+b
tU (a,b+1)=U+(a,b)-+tb
(1-α)。
式中:U(a,b)=
-α\(1-α)b
这里只考虑α与b都是整数倍的情形,这时递推初值为【1()
)={-
I(,)=,
I(1,)=V-,
I(1,1)=α,
U(,)=(1-),
U( )(),
U(1,)=
lUr(,1)=α(1-z)。
A.3.38分布分位数的计算
若参数a,b是一
-或1,由下式直接计算
GB4086.3-83
αp(
1+ tan2(号(1- p)),
1)=2,
p(1,)=1(1-p),
l cp(1,1)= p.
其它场合使用送代法计算(见GB4086.1的附录A.3),初始值由如下方法给出:rp(a,b)=
a。若α,b两参数中有一个等于,于号,则定义
t = tp*+
式中u*是与下侧概率p*对应的正态分位数,p* = -
F=2(当b=
-Yi(up*),
v=26,F=
(当a=
22(u3+u),
(5u5+ 16u3 +3u),
Y2(u)=
Y4(u)=
(3u? +19u5+17u3-15u),
(79u9 +776u? + 1482u5-1920u3- 945u),Ys(u)=
(27ull+339u9+930u?-1782u5-765u3+17955u)。213.32.5
b。若c,6两参数中没有一个等于,则定义F
式中:*=1p,c=
(1-c)(1-d)+up*(ic)2d+(1-d)2c-cdus.(1- d)2- dug*
B.1说明
GB4086.3—83
附录B
计算程序
(参考件)
这单给出用F本标准实际计第的四个FORTRAN语高了程序。它们是BFTAFD:用」计算8分布的密度函数和分布函数,BETAXD:用于计算βB分布的分位数,TFD:用于计算1分布的分布函数,TXD:用F计算t分布的分位数。
程序使用附录A的计算方法,即把t分布转化为β分布计算,因而两个分布的计算程亲是必要的此外,它们运行时又需调用两个F态分布于程序NORFD与NORXD,可参考GB4086.J的附录B:望然本标准印出的数表只取5~6位小数,但程序的计算精度通常叫达10·10程序
SUBROUTINE BETAFD(X,N2A,N2B,P,DENS)INTEGER N2A,N2B
DOUBLE PRECISION X,P,UENS
**PURPOSE**
DISTRIBUTION FUNCTION AND DENSITY OF BETA DISTRIBUTIONWITH HALF INTEGER PARAMETERS** ARGUMENTS **
ONNETRY
ON RETURN
N2A=2*A. (A-1)TH POWER OF X IN BETA DISTRIBUTIONBETF0001
BETF0002
BETF0003
BETF0004
BETF0005
BETF0006
BEIF0007
BETF0008
BETF0009
BETF0010
BETF0011
BETF0012
BETF0013
BETFO014
N2B=2*B. (B-1)TH POWER OF (1-X) IN BETA DISTRIBUTION BETF0015BETF0016
BETA POINT
RE1F0017
LOWER PROBABILITY
DENSITY
**REQUIREDROUTINES **
** ALGORITHM **
THE RECURRENCE FORMULA
I(X,A+1,B) = I(X,A,B) - (U(A.B)/A).ICX.A,B+1) = I(X,A,B) + (U(A,B)/B),U(A+1,B) = U(A.B)*X*(A + B)/A.U(A,B+1) = U(A,B)*(1-X)*(A+B)/B,WHERE
I(X.A,B) IS DISTRIBUTION FUNCTION OF BETA DISTRIBUTION.U(A,B) = X**A*(1-X)**B/BETA(A,B),BETA(A,B) IS BETA FUNCTION.
INITIAL VALUES
I(X,1/2,1/2) = 1 - (2/PAI)*ATAN(SQRI((1-X)/X)),I(X,1/2,1) = SQRI(X).
I(X,1.1/2) = 1 - SQRT(1-X).
I(X,1,1) = X,
BETF0018
BETF0019
BETF0020
BETF0021
BETF0022
REIF0023
BETF0024
BETF0025
BETF0026
BETF0027
BETF0028
BFIF0029
BEIF0030
BETF0031
BETF0032
BI.TF0033
BEIF0034
BETF005S
BETFO036
BE1F0037
BETF0038
GB4086.3--83
U(1/2.1/2)=SQRT(X(1-X))/PAI,U(1/2,1) = SQRt(X)*(1-X)/2.
U(1.1/2) = X+SQRT(1-X)/2,
U<1,1) = X(1-X).
INTEGER M,N
DOUBLEPRECISIONS.FI,FM
S = DSQRT(1.000 - X)
M = 2*(N2B/2) - N2B + 2
N = 2*(N2A/2) - N2A + 2
INITIAL VALUE
IF《M.EQ. 2)GOTO 20
IF (N .EQ. 2) G0 T0 10
N2AISODDANDN2BISODD
P = 1.0D0 - 0.63661977236758134D0*DAIAN(S/DSQRT(X))DENS=0.31830988618379067D0*S*DSQRT(X)GOTO 40
CONTINUE
N2A IS EVEN AND N28 IS 000
P = 1.000 - s
DENS = 0.500*S*X
GD TO 40
CONTINUE
IF (N .EQ. 2) GO TO 30
N2A IS ODD AND N2B IS EVEN
P = DSQRT(X)
DENS = 0.5DO*(1.0DO X)*P
GO TO 40
CONTINUE
N2A IS EVEN ANU N2B IS EVEN
DENS = X*(1.ODO X)
40 CONTINUE
SO CONTINUE
RECURRENCE
DO 60 I = N,N2A,2
IF (N2A .LE. I) GO TO 70
P = P - 2.ODO/FI*DENS
DENS = DENS*X*(FM + FI)/FI
60 CONTINUE
7O CONTINUE
DO 80 I = M.N2B,2
IF (N2B .LE. I) GO TO 90
P = P + 2.0D0/FM*BENS
DENS - DENS*(1.ODO - X)*(FM + FI)/FM80 CONTINUE
90 CONTINUE
DENS = DENS/(X*(1.ODO - X))
RETURN
BETF0039
BETF0040
BETF0041
BETF0042
BETF0Q43
BETF0044
BETF0045
BETF0046
BETF0047
BETF0048
BETF0049
BETF0050
BETF0051
BETF0052
BETF0053
BETF0054
BETF0055
BETF0056
BEIF0057
BETF0058
BETF0059
BETF0060
BETF0061
BETF0062
BETF0063
BETF0Q64
BETF006S
BETF0066
BETF0067
BETF0068
BETF0069
BETF0070
BETF0071
BETF0072
BETF0073
BETF0074
BEIF0075
BETF0076
BETF0077
BETF0078
BETF0079
BETF0080
BETF0081
BETF0082
BETF0083
BETF0084
BETF0085
BETF0086
BETF0087
BETF0088
BETF0089
BETF0090
BETF0091
BETF0092
BETFQ093
BETF0094
BETF0095
BETF0096
BETF0097
BETF0098
BETF0099
BETF0100
GB4086.3—
SUBROUTINE BETAXD(P,N2A.N28,EPS,X,IER)INTEGER N2A,N28,IER
DOUBLE PRECISION P,EPS.X
** PURPOSE **
PERCENTAGE POINT OF BETA DISTRIBUTION (INCOMPLETE BETAFUNCTION RATIO) WITH HALF INTEGER PARAMETERS** ARGUMENTS **
DN NETRY
N2A=2*A, (A-1)TH POWER OF × IN BETA DISTRIBUTIONN2A
ON RETURN
BETX0001
BETX0002
BETX0003
BETX0004
BEIX0005
BETX0006
BETX0007
BETX0008
BEIX0009
BETX0010
BETX0011
BE1X0012
BE1x0013
BETX0014
N2B=2*B, (B-1)TH POWER OF (1-X) IN BETA DISTRIBUTION BETX0015LOWER PROBABILITY
REQUIRED PRECISION
PERCENTAGE POINT
ERROR PARAMETER
IER.NE.0 INDICATES P.LE.O OR P.GE.1** REQUIRED ROUTINES **
BETAFD
PERCENTAGE POINT OF NORMAL DISTRIBUTIONDISTRIBUTION FUNCTION OF NORMAL DISTRIBUTIODISTRIBUTION FUNCTION OF BETA OISTRIBUTION**ALGORITHM **
WHEN N2A AND N2B ARE EQUAL TO 1 OR 2, THE PERCENTAGE POINTX(P,N2A/2.N28/2) IS CALCULATED BY FORMULAX(P,1/2,1/2) = 1/(1 + (TAN((PA1/2)*(1-P)))**2),X(P.1/2,2/2) = P**2,
X(P,2/2,1/2) = 1 - (1-P)**2,X(P,2/2,2/2) = P,
FOR THE OTHER UALUES OF N2A AND N2B,HITOTUMATU-S ITERATIONMETHOD IS USED, INITIAL VALUE IS CALCULATED BY YAMAUTI-SFORMULA AND PAULSON-TAKEUCHI-S FORMULA. SEE Z. YAMAUTI.STATISTICAL TABLES AND FORMULAS WITH COMPUTER APPLICATION,JSA-1972, B(2.10)-P.27, B(2.31)-P.33.INTEGER N,MN
DOUBLE PRECISION PAIS.PP,U.DENS,DDENS,R,RDOT.A.B.C.D.F1.F2DATA PAI5/1.57079632679489662D0/IER=O
IF (P .GT. 0.ODO .AND. P .LT. 1.ODO) GO TO 10IER = 129
IF (P .LE. 0.0D0) X = 0.0D0
IF (P .GE. 1.0D0) X = 1.0DO
GOTO100
1O CONTINUE
IF (N2A .GT、 2 .OR. N2B .GT. 2) GO TO 30CASE N2A=1.2 AND N2B=1,2
IF (N2A .EQ. 1 ,AND. N2B -EQ. 1) X = 1.0D0/(1.0D0 +(DSIN(PAI5*(1.ODO-P))/DCOS(PAI5*(1. ODO-P)))**2)IF (N2A .EQ. 1 .AND. N?B .EQ. 2) X = P**2BETX0016
BETX0017
BETX0018
BETX0019
BETX0020
BEIX0021
BEIX0022
BETX0023
BE1X0024
BETX0025
BETX0026
BETX0027
BETX0028
BETX0029
BETX0030
BETX0031
BETX0032
8E1X0033
BETX0034
BETX0035
BETX0036
BETX0037
BEIX0038
BETX0039
BETX0040
BETX0041
BETX0042
BETX0043
BETX0044
BEiX0045
BETX0046
BETX0047
BETX0048
BETX0049
BETX0050
BETX0051
BETX0052
BEIX0053
BEIX0054
BETX0055
BETX0056
BE1X0057
BEIX0058
BEIXOS9
BETX0060
BETXOCG1
BETX0062
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。