GB/Z 26958.30-2017
基本信息
标准号: GB/Z 26958.30-2017
中文名称:产品几何技术规范(GPS) 滤波 第30部分:稳健轮廓滤波器 基本概念
标准类别:国家标准(GB)
标准状态:现行
出版语种:简体中文
下载格式:.rar .pdf
下载大小:995KB
相关标签: 产品 几何 技术规范 滤波 轮廓 滤波器 基本概念

标准分类号
关联标准
出版信息
相关单位信息
标准简介
GB/Z 26958.30-2017 产品几何技术规范(GPS) 滤波 第30部分:稳健轮廓滤波器 基本概念
GB/Z26958.30-2017
标准压缩包解压密码:www.bzxz.net
标准图片预览




标准内容
ICS17.040.20
中华人民共和国国家标准化指导性技术文件GB/Z26958.30—2017/ISO/TS16610-30:2009产品几何技术规范(GPS)
第30部分:稳健轮廓滤波器
基本概念
Geometrical product specifications (GPS)Filtration-Part3o:RobustprofilefiltersBasicconcept(ISO/TS16610-30:2009.IDT)
2017-02-28发布
中华人民共和国国家质量监督检验检疫总局中国国家标准化管理委员会
2017-09-01实施
GB/Z26958.30—2017/ISO/TS16610-30:2009前言
GB/Z26958《产品几何技术规范(GPS)滤波》已发布的有以下10个部分:第1部分:概述和基本概念;
一第20部分:线性轮廓滤波器
基本概念;
第22部分:线性轮廓滤波器
样条滤波器;
第29部分:线性轮廓滤波器
样条小波;
基本概念;
一第30部分:稳健轮廓滤波器
第31部分:稳健轮廊滤波器
第32部分:稳健轮廓滤波器
高斯回归滤波器;
样条滤波器;
第40部分:形态学轮廓滤波器
第41部分:形态学轮廓滤波器
第49部分:形态学轮廓滤波器
本部分为GB/Z26958的第30部分。基本概念;
圆盘和水平线段滤波器;
尺度空间技术。
本部分按照GB/T1.1一2009给出的规则起草本部分使用翻译法等同采用ISO/TS16610-30:2009《产品几何技术规范(GPS)滤波第30部分:稳健轮廓滤波器基本概念》。GB/Z26958对应ISO/TS16610,目前ISO/TS16610包括89个部分,已转化为国家标准指导性技术文件的有以上10个部分。
请注意本文件的某些内容可能涉及专利。本文件的发布机构不承担识别这些专利的责任。本部分由全国产品几何技术规范标准化技术委员会(SAC/TC240)提出并归口。本部分起草单位:中机生产力促进中心、哈尔滨量具刃具集团有限责任公司、华中科技大学、北京时代之峰科技有限公司、中国计量学院本部分主要起草人:明翠新、郎岩梅、刘晓军、张彦春、赵军、陈景玉。1
1范围
GB/Z26958.30—2017/ISO/TS16610-30:2009产品几何技术规范(GPS)
第30部分:稳健轮廓滤波器
GB/Z26958的本部分规定了稳健轮廓滤波器的基本概念。2规范性引用文件
基本概念
下列文件对于本文件的应用是必不可少的。凡是注日期的引用文件,仅注日期的版本适用于本文件。凡是不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件GB/Z26958.1一2011产品几何技术规范(GPS)滤波第1部分:概述和基本概念(ISO/TS16610-1:2006,IDT)
GB/Z26958.20—2011产品几何技术规范(GPS)滤波第20部分:线性轮廓滤波器基本概
念(ISO/TS16610—20:2006.IDT)ISO/IEC指南99:2007国际计量学词汇基本和通用概念和术语[Internationalvocabularyofmetrology-Basic and general concepts and associated terms (VIM))3术语和定义
ISO/IEC指南99、GB/Z26958.1和GB/Z26958.20界定的以及下列术语和定义适用于本文件。3.1
稳健性
robustness
输出数据对输人数据中特殊现象的不敏感性。注:特殊现象如异常值、划伤,台阶等。[GB/Z26958.1,定义3.9]。
轮廓不连续
profilediscontinuity
轮廓特性发生突变的轮廓部分。3.2.1
斜率不连续
slopediscontinuity
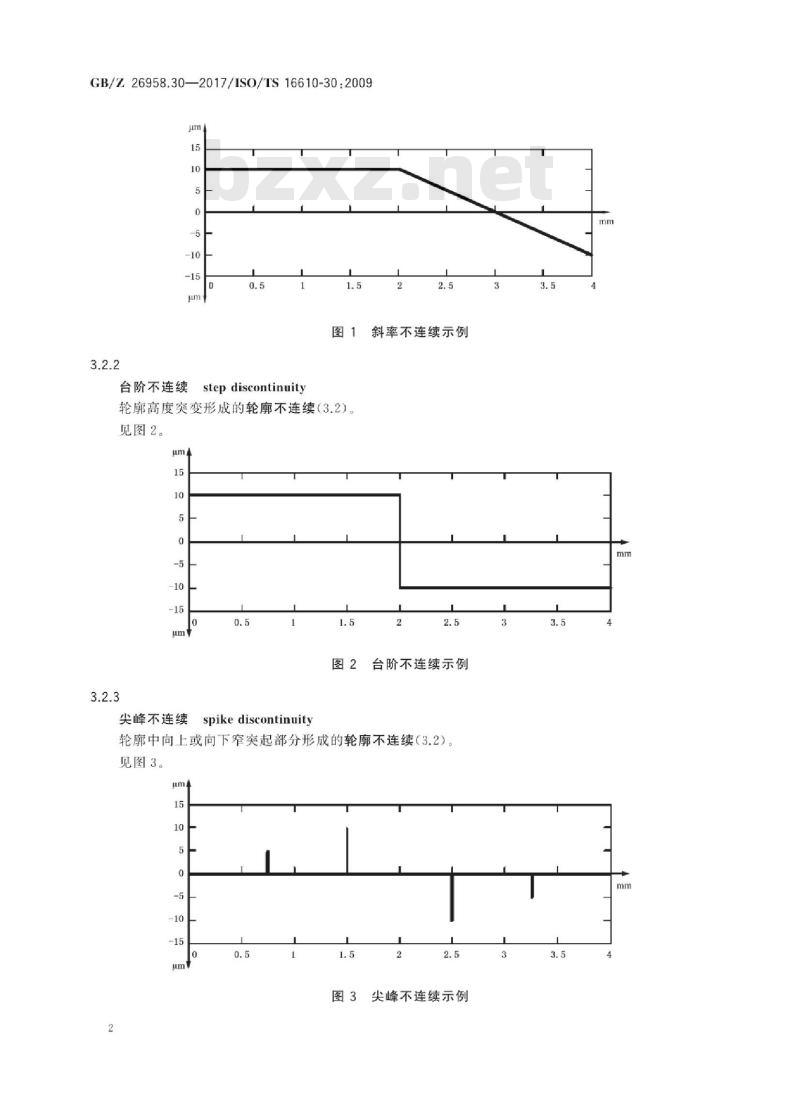
轮廓斜率突变形成的轮廓不连续(3.2)。见图1。
GB/Z26958.30—2017/ISO/TS16610-30:2009um
台阶不连续
step discontinuity
斜率不连续示例
轮廓高度突变形成的轮廓不连续(3.2)。见图2。
尖峰不连续
spike discontinuity
台阶不连续示例
轮廓中向上或向下窄突起部分形成的轮廓不连续(3.2)。见图3。
μum a
尖峰不连续示例
度量metric
<轮廓法》满足以下三个条件的两轮廓间的特性:GB/Z26958.30—2017/ISO/TS16610-30:2009正定性,即(()())≥0,当且仅当()=()时等号成立交换性即(().())=(()())
三角不等性即()()+((≥(()()式中:
()是两个轮廓P1和2的函数,其结果为一个实数。3.3.1
<轮廓法>用来定义某一度量(3.3)的两个轮廓的函数。3.3.2
L1-范数L1-norm
连续绝对偏差范数
continuous absolute deviation norm<轮廓法>由以下积分公式定义的范数(3.3.1):(i().())
11-范数11-norm
()-2()d
离散绝对偏差范数
discreteabsolutedeviationnorm<轮廓法>由以下求和公式定义的范数(3.3.1):8(pi()p2(α))-
L2-范数L2-norm
连续最小二乘范数
Ipi(.)-p2(a)
continuous least squares norm<轮廓法>由以下积分公式定义的范数(3.3.1):(().()
12-范数12-norm
离散最小二乘范数
(pi()pa())da
discrete least squares norm
<轮廓法>由以下求和公式定义的范数(3.3.1):(pi().(α))=
Loo-norm
Loo-范数
(pr(a:)-p2(a))
连续切比雪夫范数
continuous Chebychey norm
轮廓法由以下公式定义的范数(3.3.1):8(()2()=
[80-范数
Joo-norm
GB/Z26958.30—2017/ISO/TS16610-30:2009离散切比雪夫范数
discrete Chebychev norm
<轮廓法>由以下公式定义的范数(3.3.1):(pi(a)p(a))
统计估计statisticalestimatorIp()—()
基于由总体抽取的样本数据作出的估计。3.4.1
稳健统计估计robust statistical estimator对输入数据中的特殊现象不敏感的统计估计(3.4)。3.5
M-估计
M-estimator
根据数据点偏离基准线的带符号距离,使用影响函数(3.5.1)对数据加权的稳健统计估计(3.4.1)。3.5.1
影响函数
influencefunction
不对称且尺寸不变的函数。
注1:如果数据中某点的值用任意值替换,该改变点对M-估计(3.5)结果的影响与影响函数成比例。注2:要满足尺度不变,需要给影响函数确定一个尺度参数。轮廓相对于基准线离散性的估计值如中值绝对偏差(3.5.2)可用来确定尺度参数。
中值绝对偏差
median absolute deviation
表征系列观测值离散性的一个参数,它对于尖峰不连续(3.2.3)稳健,可通过计算每个观测值到所有观测值中值的绝对偏差的中值得到。注1:对于高斯概率分布,标准偏差等于1.4826×MAD,注2:关于中值的更多信息,见参考文献[9]和参考文献[10]。见图4。
注:a)为平均值:b)为中值;c)为胡贝尔(Huber)函数:d)为双权函数。1
图4与M估计相关的影响函数示例4
贝叶斯估计Bayesianestimator
GB/Z26958.30—2017/ISO/TS16610-30:2009根据各数据点到基准线的带符号距离采用贝叶斯统计加权的稳健统计估计(3.4.1)。4稳健性
4.1概述
稳健性不是一般意义的轮廓滤波器的绝对特性,而是一个相对特性。若输人数据中的特殊现象在一种轮廓滤波器的响应输出中引起的失真比其在另一种轮廓滤波器响应输出中引起的失真更小,则说明这种轮廓滤波器对于这种特殊现象比另一种轮廓滤波器更稳健为广使稳健性成为轮廓滤波器的绝对特性,需要定义一个轮郭滤波器稳健性的参考归类。本技术规范中采用的轮廓滤波器的参考归类是线性轮廓滤波器(GB/Z26958.20)。根据定义,所有稳健轮廓滤波器在其应用中有非线性部分。有几项知名技术可以构建对于一种特殊现象的稳健滤波器(皆为非线性),具体见4.2、4.3、4.3.1、4.3.2、4.4、4.4.1、4.4.2。4.2基于度量的方法
这里,用于滤波后轮廓贴合原轮廓的度量是一种更稳健的度量。例如,对于尖峰不连续,基于L1-范数的度量比基于最小二乘范数(L2-范数)的度量更稳健,而基于L2-范数的度量比基于切比雪夫范数(Lo-范数)的度量更稳健注:与这些度量等效的粗糙度参数为Ra(L1-范数)、Rq(L2-范数)、Rz(Loo-范数)。这些参数对于轮廊中变化的敏感性呈递增趋势。免费标准下载网bzxz
4.3基于统计法的方法
4.3.1概述
在本部分,只有M估计和贝叶斯估计用作基于统计学方法来确定轮廓的稳健滤波器,当然可能还有其他方法存在。
4.3.2M估计
轮廓上的每一点根据一个影响函数有不同的权重,此影响函数用轮廓滤波器的低通响应作为基准线。由此,远离低通响应的各点比接近低通响应的点有更小的相对权重。这种方法使滤波后的轮廓对尖峰不连续更加稳健。在关于稳健统计学的标准文献中,可以找到几种常用的影响函数来分配各点权重厂胡贝尔(Huber),比顿(Beaton)函数等注:这种稳健性方法通常用选代法实现,因为计算权重需要轮廓滤波器的响应。4.3.3贝叶斯(Bayesian)估计
建立一个统计模型,表达轮廓的典型成分和尖峰不连续成分。首先得到各种成分的分布,然后用贝叶斯法计算轮廓的每一点是尖峰不连续还是轮廓的典型点的概率,并据此给定每一点权重,最后用与M估计相似的方法,用这些点的权重得到滤波后轮廓。4.4预处理法
4.4.1概述
预处理是在滤波前用其他方法去除或大幅减小轮廊中不希望成分的技术,这样消除或极大减小不5
GB/Z26958.30—2017/ISO/TS16610-30:2009希望成分对轮廓滤波器响应的影响。换言之,预处理后再进行滤波,就可以达到稳健滤波的效果。这种方法的优点是,一旦找到一种去除不需要成分的方法,就可以将其与任意轮廓滤波器组合使用。4.4.2尺度空间预处理
尺度空间技术(GB/Z26958.49)可用来在滤波前去除轮廓不连续。通过对尺度空间的每个尺度设置硬阈值以上系数,来识别轮廓的不连续。通过将设置的硬阈值以上系数置零,可以去除轮廓的不连续,并重构轮廓。尺度空间预处理允许所有轮廓滤波器对轮廓不连续都是稳健的4.4.3小波预处理
可以用小波(GB/Z26958.29)在滤波前去除轮廓不连续。通过对尺度小波空间的每个层次设置硬闯值以上系数,来识别轮廓的不连续。通过将设置的硬阐值以上系数置零,可以去除轮廓的不连续,并重构轮廓。小波预处理允许所有轮廓滤波器对轮廓不连续都是稳健的。A.1概述
GB/Z26958.30—2017/ISO/TS16610-30:2009附录A
(资料性附录)
说明性数据集一
轮廓不连续的输入
轮廓滤波器的一个重要特性是其对轮廓不连续的响应方式。此处讨论的轮廓不连续的三种基本类型为:斜率不连续、台阶不连续、尖峰不连续。A.2斜率不连续
斜率不连续数据集的定义如下:当0当2当X为其他值,Z无定义
X间距为0.5μm。
图1为此类数据集的一个示例、
图A.1说明了对斜率不连续数据集施加ISO/TS16610-21规定的高斯滤波器,截止波长为0.8mm;图A.2为原始轮廓与滤波轮廓的差别。μum t
对斜率不连续数据集滤波示例
GB/Z26958.30—2017/ISO/TS16610-30:2009μmt
台阶不连续
斜率不连续数据集的原始轮廓与滤波轮廓间差值的示例台阶不连续数据集的定义如下:当0当2当X为其他值,z无定义。
X间距为0.5μm。
图2为此类数据集的一个示例。
图A.3说明了对台阶不连续数据集施加ISO/TS16610-21规定的高斯滤波器,截止波长为0.8mm。
台阶不连续数据集滤波示例
A.4尖峰不连续
尖峰不连续数据集的定义如下:当0当X=0.75.z=5am
当X=1.5,z=10μm
当X=2.5.z=-10μm
当X=3.25.Z=-5μm
当X为其他值,Z无定义
X间距为0.5μm。
图3为此类数据集的一个示例。
GB/Z26958.30—2017/ISO/TS16610-30:2009图A.4说明了对尖峰不连续数据集施加ISO/TS16610-21规定的高斯滤波器,截止波长为o.8mm.
尖峰不连续数据集滤波示例
GB/Z26958.30—2017/ISO/TS16610-30:2009附录B
(资料性附录)
概念图
见图B.1。
3.2.1斜率不连续
3.2轮廊
不连续
M-估计
健统计
3.1稳健
3.2.2台阶不连续
3.2.3尖峰不连续
3.5.2中值绝对偏差
3.5.1影响函数
3.3.1范数
3.3度量
概念图
3.3.2L1-范数
3.3.311-范数
3.3.4L2-范数
3.3.512-范数
3.3.6Leo-范数
3.3.7100-范数
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。
中华人民共和国国家标准化指导性技术文件GB/Z26958.30—2017/ISO/TS16610-30:2009产品几何技术规范(GPS)
第30部分:稳健轮廓滤波器
基本概念
Geometrical product specifications (GPS)Filtration-Part3o:RobustprofilefiltersBasicconcept(ISO/TS16610-30:2009.IDT)
2017-02-28发布
中华人民共和国国家质量监督检验检疫总局中国国家标准化管理委员会
2017-09-01实施
GB/Z26958.30—2017/ISO/TS16610-30:2009前言
GB/Z26958《产品几何技术规范(GPS)滤波》已发布的有以下10个部分:第1部分:概述和基本概念;
一第20部分:线性轮廓滤波器
基本概念;
第22部分:线性轮廓滤波器
样条滤波器;
第29部分:线性轮廓滤波器
样条小波;
基本概念;
一第30部分:稳健轮廓滤波器
第31部分:稳健轮廊滤波器
第32部分:稳健轮廓滤波器
高斯回归滤波器;
样条滤波器;
第40部分:形态学轮廓滤波器
第41部分:形态学轮廓滤波器
第49部分:形态学轮廓滤波器
本部分为GB/Z26958的第30部分。基本概念;
圆盘和水平线段滤波器;
尺度空间技术。
本部分按照GB/T1.1一2009给出的规则起草本部分使用翻译法等同采用ISO/TS16610-30:2009《产品几何技术规范(GPS)滤波第30部分:稳健轮廓滤波器基本概念》。GB/Z26958对应ISO/TS16610,目前ISO/TS16610包括89个部分,已转化为国家标准指导性技术文件的有以上10个部分。
请注意本文件的某些内容可能涉及专利。本文件的发布机构不承担识别这些专利的责任。本部分由全国产品几何技术规范标准化技术委员会(SAC/TC240)提出并归口。本部分起草单位:中机生产力促进中心、哈尔滨量具刃具集团有限责任公司、华中科技大学、北京时代之峰科技有限公司、中国计量学院本部分主要起草人:明翠新、郎岩梅、刘晓军、张彦春、赵军、陈景玉。1
1范围
GB/Z26958.30—2017/ISO/TS16610-30:2009产品几何技术规范(GPS)
第30部分:稳健轮廓滤波器
GB/Z26958的本部分规定了稳健轮廓滤波器的基本概念。2规范性引用文件
基本概念
下列文件对于本文件的应用是必不可少的。凡是注日期的引用文件,仅注日期的版本适用于本文件。凡是不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件GB/Z26958.1一2011产品几何技术规范(GPS)滤波第1部分:概述和基本概念(ISO/TS16610-1:2006,IDT)
GB/Z26958.20—2011产品几何技术规范(GPS)滤波第20部分:线性轮廓滤波器基本概
念(ISO/TS16610—20:2006.IDT)ISO/IEC指南99:2007国际计量学词汇基本和通用概念和术语[Internationalvocabularyofmetrology-Basic and general concepts and associated terms (VIM))3术语和定义
ISO/IEC指南99、GB/Z26958.1和GB/Z26958.20界定的以及下列术语和定义适用于本文件。3.1
稳健性
robustness
输出数据对输人数据中特殊现象的不敏感性。注:特殊现象如异常值、划伤,台阶等。[GB/Z26958.1,定义3.9]。
轮廓不连续
profilediscontinuity
轮廓特性发生突变的轮廓部分。3.2.1
斜率不连续
slopediscontinuity
轮廓斜率突变形成的轮廓不连续(3.2)。见图1。
GB/Z26958.30—2017/ISO/TS16610-30:2009um
台阶不连续
step discontinuity
斜率不连续示例
轮廓高度突变形成的轮廓不连续(3.2)。见图2。
尖峰不连续
spike discontinuity
台阶不连续示例
轮廓中向上或向下窄突起部分形成的轮廓不连续(3.2)。见图3。
μum a
尖峰不连续示例
度量metric
<轮廓法》满足以下三个条件的两轮廓间的特性:GB/Z26958.30—2017/ISO/TS16610-30:2009正定性,即(()())≥0,当且仅当()=()时等号成立交换性即(().())=(()())
三角不等性即()()+((≥(()()式中:
()是两个轮廓P1和2的函数,其结果为一个实数。3.3.1
<轮廓法>用来定义某一度量(3.3)的两个轮廓的函数。3.3.2
L1-范数L1-norm
连续绝对偏差范数
continuous absolute deviation norm<轮廓法>由以下积分公式定义的范数(3.3.1):(i().())
11-范数11-norm
()-2()d
离散绝对偏差范数
discreteabsolutedeviationnorm<轮廓法>由以下求和公式定义的范数(3.3.1):8(pi()p2(α))-
L2-范数L2-norm
连续最小二乘范数
Ipi(.)-p2(a)
continuous least squares norm<轮廓法>由以下积分公式定义的范数(3.3.1):(().()
12-范数12-norm
离散最小二乘范数
(pi()pa())da
discrete least squares norm
<轮廓法>由以下求和公式定义的范数(3.3.1):(pi().(α))=
Loo-norm
Loo-范数
(pr(a:)-p2(a))
连续切比雪夫范数
continuous Chebychey norm
轮廓法由以下公式定义的范数(3.3.1):8(()2()=
[80-范数
Joo-norm
GB/Z26958.30—2017/ISO/TS16610-30:2009离散切比雪夫范数
discrete Chebychev norm
<轮廓法>由以下公式定义的范数(3.3.1):(pi(a)p(a))
统计估计statisticalestimatorIp()—()
基于由总体抽取的样本数据作出的估计。3.4.1
稳健统计估计robust statistical estimator对输入数据中的特殊现象不敏感的统计估计(3.4)。3.5
M-估计
M-estimator
根据数据点偏离基准线的带符号距离,使用影响函数(3.5.1)对数据加权的稳健统计估计(3.4.1)。3.5.1
影响函数
influencefunction
不对称且尺寸不变的函数。
注1:如果数据中某点的值用任意值替换,该改变点对M-估计(3.5)结果的影响与影响函数成比例。注2:要满足尺度不变,需要给影响函数确定一个尺度参数。轮廓相对于基准线离散性的估计值如中值绝对偏差(3.5.2)可用来确定尺度参数。
中值绝对偏差
median absolute deviation
表征系列观测值离散性的一个参数,它对于尖峰不连续(3.2.3)稳健,可通过计算每个观测值到所有观测值中值的绝对偏差的中值得到。注1:对于高斯概率分布,标准偏差等于1.4826×MAD,注2:关于中值的更多信息,见参考文献[9]和参考文献[10]。见图4。
注:a)为平均值:b)为中值;c)为胡贝尔(Huber)函数:d)为双权函数。1
图4与M估计相关的影响函数示例4
贝叶斯估计Bayesianestimator
GB/Z26958.30—2017/ISO/TS16610-30:2009根据各数据点到基准线的带符号距离采用贝叶斯统计加权的稳健统计估计(3.4.1)。4稳健性
4.1概述
稳健性不是一般意义的轮廓滤波器的绝对特性,而是一个相对特性。若输人数据中的特殊现象在一种轮廓滤波器的响应输出中引起的失真比其在另一种轮廓滤波器响应输出中引起的失真更小,则说明这种轮廓滤波器对于这种特殊现象比另一种轮廓滤波器更稳健为广使稳健性成为轮廓滤波器的绝对特性,需要定义一个轮郭滤波器稳健性的参考归类。本技术规范中采用的轮廓滤波器的参考归类是线性轮廓滤波器(GB/Z26958.20)。根据定义,所有稳健轮廓滤波器在其应用中有非线性部分。有几项知名技术可以构建对于一种特殊现象的稳健滤波器(皆为非线性),具体见4.2、4.3、4.3.1、4.3.2、4.4、4.4.1、4.4.2。4.2基于度量的方法
这里,用于滤波后轮廓贴合原轮廓的度量是一种更稳健的度量。例如,对于尖峰不连续,基于L1-范数的度量比基于最小二乘范数(L2-范数)的度量更稳健,而基于L2-范数的度量比基于切比雪夫范数(Lo-范数)的度量更稳健注:与这些度量等效的粗糙度参数为Ra(L1-范数)、Rq(L2-范数)、Rz(Loo-范数)。这些参数对于轮廊中变化的敏感性呈递增趋势。免费标准下载网bzxz
4.3基于统计法的方法
4.3.1概述
在本部分,只有M估计和贝叶斯估计用作基于统计学方法来确定轮廓的稳健滤波器,当然可能还有其他方法存在。
4.3.2M估计
轮廓上的每一点根据一个影响函数有不同的权重,此影响函数用轮廓滤波器的低通响应作为基准线。由此,远离低通响应的各点比接近低通响应的点有更小的相对权重。这种方法使滤波后的轮廓对尖峰不连续更加稳健。在关于稳健统计学的标准文献中,可以找到几种常用的影响函数来分配各点权重厂胡贝尔(Huber),比顿(Beaton)函数等注:这种稳健性方法通常用选代法实现,因为计算权重需要轮廓滤波器的响应。4.3.3贝叶斯(Bayesian)估计
建立一个统计模型,表达轮廓的典型成分和尖峰不连续成分。首先得到各种成分的分布,然后用贝叶斯法计算轮廓的每一点是尖峰不连续还是轮廓的典型点的概率,并据此给定每一点权重,最后用与M估计相似的方法,用这些点的权重得到滤波后轮廓。4.4预处理法
4.4.1概述
预处理是在滤波前用其他方法去除或大幅减小轮廊中不希望成分的技术,这样消除或极大减小不5
GB/Z26958.30—2017/ISO/TS16610-30:2009希望成分对轮廓滤波器响应的影响。换言之,预处理后再进行滤波,就可以达到稳健滤波的效果。这种方法的优点是,一旦找到一种去除不需要成分的方法,就可以将其与任意轮廓滤波器组合使用。4.4.2尺度空间预处理
尺度空间技术(GB/Z26958.49)可用来在滤波前去除轮廓不连续。通过对尺度空间的每个尺度设置硬阈值以上系数,来识别轮廓的不连续。通过将设置的硬阈值以上系数置零,可以去除轮廓的不连续,并重构轮廓。尺度空间预处理允许所有轮廓滤波器对轮廓不连续都是稳健的4.4.3小波预处理
可以用小波(GB/Z26958.29)在滤波前去除轮廓不连续。通过对尺度小波空间的每个层次设置硬闯值以上系数,来识别轮廓的不连续。通过将设置的硬阐值以上系数置零,可以去除轮廓的不连续,并重构轮廓。小波预处理允许所有轮廓滤波器对轮廓不连续都是稳健的。A.1概述
GB/Z26958.30—2017/ISO/TS16610-30:2009附录A
(资料性附录)
说明性数据集一
轮廓不连续的输入
轮廓滤波器的一个重要特性是其对轮廓不连续的响应方式。此处讨论的轮廓不连续的三种基本类型为:斜率不连续、台阶不连续、尖峰不连续。A.2斜率不连续
斜率不连续数据集的定义如下:当0
X间距为0.5μm。
图1为此类数据集的一个示例、
图A.1说明了对斜率不连续数据集施加ISO/TS16610-21规定的高斯滤波器,截止波长为0.8mm;图A.2为原始轮廓与滤波轮廓的差别。μum t
对斜率不连续数据集滤波示例
GB/Z26958.30—2017/ISO/TS16610-30:2009μmt
台阶不连续
斜率不连续数据集的原始轮廓与滤波轮廓间差值的示例台阶不连续数据集的定义如下:当0
X间距为0.5μm。
图2为此类数据集的一个示例。
图A.3说明了对台阶不连续数据集施加ISO/TS16610-21规定的高斯滤波器,截止波长为0.8mm。
台阶不连续数据集滤波示例
A.4尖峰不连续
尖峰不连续数据集的定义如下:当0
当X=1.5,z=10μm
当X=2.5.z=-10μm
当X=3.25.Z=-5μm
当X为其他值,Z无定义
X间距为0.5μm。
图3为此类数据集的一个示例。
GB/Z26958.30—2017/ISO/TS16610-30:2009图A.4说明了对尖峰不连续数据集施加ISO/TS16610-21规定的高斯滤波器,截止波长为o.8mm.
尖峰不连续数据集滤波示例
GB/Z26958.30—2017/ISO/TS16610-30:2009附录B
(资料性附录)
概念图
见图B.1。
3.2.1斜率不连续
3.2轮廊
不连续
M-估计
健统计
3.1稳健
3.2.2台阶不连续
3.2.3尖峰不连续
3.5.2中值绝对偏差
3.5.1影响函数
3.3.1范数
3.3度量
概念图
3.3.2L1-范数
3.3.311-范数
3.3.4L2-范数
3.3.512-范数
3.3.6Leo-范数
3.3.7100-范数
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。