本标准规定了天然气、含人工掺合物的天然气和其他类似混合物仅以气体状态存在时的压缩因子计算方法。 GB/T 17747.3-1999 天然气压缩因子的计算 第3部分：用物性值进行计算 GB/T17747.3-1999 标准下载解压密码：www.bzxz.net

GB/T17747.3—1999
本标准等效采用1SO12213-3:1997《天然气压缩因子的计算用物性值进行计算》。本标准在技术内容和编写格式上与ISO12213-3：1997完全-一致。本标准取消了国际标准的附录F和附录G。本标准中高位发热量和相对密度采用的参比条件同我国石油气体所采用的标准参比条件不同，为方便使用，在4.4.1和4.4.2增加了注2和注3，在附录D的表D1和表D4中补充了我国石油气体规定的标准参比条件和同本标准采用的参比条件间的换算关系式。《天然气压缩因子的计算》标准包括以下3个部分：第1部分《导论和指南》；第2部分《用摩尔组成进行计算》；第3部分《用物性值进行计算》。本标准是第3部分（GB/T17747.3---1999）：用物性值进行计算。
本标准的附录A、附录B、附录C、附录D是标准的附录。本标准的附录E是提示的附录。
本标准由原中国石油天然气总公司提出。本标准由石油工业天然气专业标准化技术委员会归口并负责解释。本标准起草单位：中国石油天然气集团公司四川石油管理局天然气研究院。本标准主要起草人：罗勤、陈魔良、曾文平、许文晓、富朝英、陈荣松。GB/T 17747.3—1999
ISO前言
ISO（国际标准化组织）是各国家标准化机构（ISO成员）组成的世界性的联合会。制定国际标准的工作通常由ISO技术委员会完成。对技术委员会提出的项目感兴趣的每个成员都有权参加。与ISO保持联系的各政府或非政府的国际性组织也可以参加此项工作。所有电工技术方面的标准化工作，ISO与IEC(国际电工委员会)保持密切的合作。由技术委员会通过的国际标准草案交各成员进行表决投票，要求至少有75%的成员同意，才能作为国际标准正式发布。
国际标准ISO12213-3是由天然气技术委员会ISO/TC193下的天然气分析”分委员会制定的。ISO12213\天然气压缩因子的计算”标准包括以下3个部分：第1部分：导论和指南；
第2部分：用摩尔组成进行计算；第3部分：用物性值进行计算。
附录 A、附录B、附录 C、附录 D是标准的附录。附录 E、附录 F、附录 G是提示的附录。373
1范围
中华人民共和国国家标准
天然气压缩因子的计算
第3部分：用物性值进行计算
Natural gasCalculation of compression factor-Part 3:Calculation using physical propertiesGB/T17747.3—1999
eqv ISO 12213-3:1997
本标准规定了天然气、含人工掺合物的天然气和其他类似混合物仅以气体状态存在时的压缩因子计算方法。该计算方法是用已知的高位发热量、相对密度和CO，含量及相应的压力和温度计算气体的压缩因子。如果存在H2，也需知道其含量，在含人工掺合物的气体中常有这种情况。注 1：已知高位发热量、相对密度、CO，含量和N2含量中任意三个变量时，即可计算压缩因子。但 N2含量作为输人变量之一的计算方法不作为推荐方法，一般是使用前面三个变量作为计算的输人变量。该计算方法又称为SGERG-88计算方法，主要应用于在输气和配气正常进行的压力p和温度T范围内的管输气，不确定度约为士0.1%。也可用于更宽范围，但计算结果的不确定度会增加（见附录E）。有关该计算方法应用范围和应用领域更详细的说明见GB/T17747.1。2引用标准
下列标准所包含的条文，通过在本标准中引用而构成为本标准的条文。本标准出版时，所示版本均为有效。所有标准都会被修订，使用本标准的各方应探讨使用下列标准最新版本的可能性。GB/T3102.3-—1993力学的量和单位GB/T3102.4—1993热学的量和单位GB/T110621998天然气发热量、密度、相对密度和沃泊指数的计算方法（neqISO6976：1995）GB/T17747.1--1999天然气压缩因子的计算第1部分：导论和指南（eqvISO12213-1：1997）GB/T17747.2-1999天然气压缩因子的计算第2部分：用靡尔组成进行计算（eqvISO12213-2:1997)
3定义
相关于本标准的所有定义见GB/T17747.1。文中出现的符号所代表的含义及单位见附录A。4计算方法
4.1原理
SGERG-88计算方法所使用的方程是基于这样的概念：管输天然气的容量性质可由一组合适的、特征的、可测定的物性值来表征和计算。这些特征的物性值与压力和温度一起作为计算方法的输人数据。该计算方法使用高位发热量、相对密度和CO2含量作为输人变量。尤其适用于无法得到气体摩尔全组成的情况，它的优越之处还在于计算相对简单。对含人工掺合物的气体，需知道H，的含量。4.2SGERG-88方程
国家质量技术监督局1999-05-17批准37.4
1999-12-01实施
GB/T17747.3—1999
SGERG-88计算方法是基于GERG-88标推维利方程（表示为SGERG-88方程，见GB/T17747.1）。该SGERG-88方程是由MGERG-88维利方程推导出来的。MGERG-88方程是基于摩尔组成的计算方法。
SGERG-88方程可写作：
Z= 1→+ Bpm + Cpm
式中：B、C
高位发热量（H.）、相对密度（d）、气体混合物中不可燃和可燃的非烃组分（CO2、H2)的含量及温度(T)的函数；
摩尔密度。
pm由方程（2)得出：
Pm = p/(ZRT)
式中：
Z = fi(p,T,H.,d,xco,,xH,)
...(2)
（3）
SGERG-88计算方法把天然气混合物看成本质上是由等价烃类气体（其热力学性质与存在的烃类的热力学性质总和相等）、N2、CO2、H2和CO组成的五组分混合物。为了充分表征烃类气体的热力学性质，还需要知道烃类的发热量HcH，压缩因子Z的计算公式如下：Z = fz(p,T,HcH,cH,N,,co, H,&co)..(4)
为了能模拟焦炉混合气，一般所采用的CO摩尔分数与H，含量存在一个固定的比例关系。若不存在H2（aH,<0.001),则设H，一0；这样在计算中可将天然气混合物看成是由三个组分组成的混合物（见附录B)。
计算按三个步骤进行：首先，根据附录B描述的选代程序，通过输人数据得到同时满足已知高位发热量和相对密度的五种组分的组成。其次，按附录B给出的关系式求出B和C。最后，用适宜的数值计算方法求解联立方程（1)和（2),得到0m和Z。由输人数据计算压缩因子Z的计算程序流程见附录B中的图B1。4.3输人变量
4.3.1优先选择的输人数据组
SGERG-88计算方法的输人变量包括绝对压力、热力学温度和高位发热量（体积基）、相对密度、CO2 含量及 H2 含量。用作输入数据组(A 组)的物性值有：H.、d、αco, 和 zH,(A组);
相对密度指GB/T 17747.1-1999的 3.6规定参比条件下的相对密度。高位发热量指GB/T17747.1-1999的3.5规定参比条件下的高位发热量。4.3.2可选择的输人数据组
除4.3.1中优先选择的输入数据组（A)之外，还有其他三组可选择的输人数据用于SGERG-88计算方法：
N,Hsd 和 xH,(B组);
TN cO,d 和 ZH,(C 组);
N,CO,H, 和 H,(D组);
用以上输入数据组得到的计算结果仅在小数后第四位上可能有差异。本标准推荐使用输人数据组(A)。
4.4应用范围
4.4.1管输气
SGERG-88计算方法对管输气的应用范围如下：绝对压力：
0 MPa热力学温度：
CO，的摩尔分数：
Hz的摩尔分数：
高位发热量：
相对密度：
GB/T17747.3-1999
263K≤T<338K
0≤xco. ≤0. 20
0≤H,≤0. 10
30MJ·m-3≤H.≤45MJm-3
0.55≤d≤0.80
注2：将本条中的高位发热量和相对密度换算为我国石油气体标准参比条件下的高位发热量和相对密度，则高位发热量范围为27.95~41.93MJ·m2°，相对密度范围为0.550~0.800。天然气中其他组分的摩尔分数不作为输人数据。但是，他们必须在下列范围之内：CH4:
CHio：
C,Hi6:
C.H18和更高碳数烃类：
0. 7≤CH,≤1. 0
0αN,0.20
0αc,H,0.10
0≤c,H,0.035
0≤xc,H。≤0. 015
0≤c,H0. 005
0≤c,≤0.001
0≤c,0. 000 5
0rc0.0005
0He≤0.005
0≤xH,0≤0.000 15
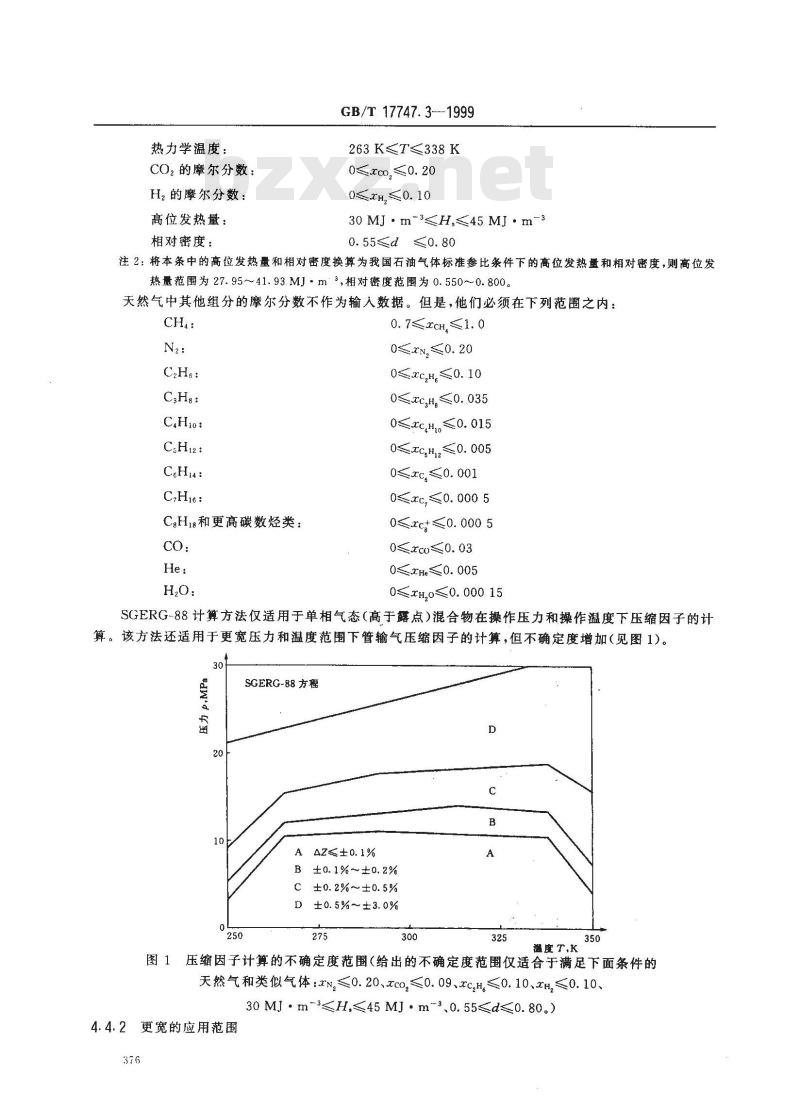
SGERG-88计算方法仅适用于单相气态（高于露点）混合物在操作压力和操作温度下压缩因子的计算。该方法还适用于更宽压力和温度范围下管输气压缩因子的计算，但不确定度增加（见图1)。SGERG-88 方程
A AZ≤±0.1%
B ±0. 1% ~±0.2%
C ±0. 2%~±0. 5%
D ±0.5%~±3. 0%
温度 T,K
图1压缩因子计算的不确定度范围(给出的不确定度范围仅适合于满足下面条件的天然气和类似气体：zN≤0.20、cco,≤0.09、xc,H。≤0.10、2H,≤0.10、30MJ·m~3≤H,≤45MJ·m-30.55≤d≤0.80。)4.4.2
更宽的应用范围
GB/T 17747.3—1999
超出4.4.1所给出范围的应用范围如下：绝对压力：
热力学温度：
CO2的摩尔分数：
H2的摩尔分数：
高位发热量：
相对密度：
0 MPa263 K≤T≤338 K
0≤xco,≤0.30
0≤xH,≤0.10
20 MJ ·m-30.55≤d≤0.90
注3：将本条中的高位发热量和相对密度换算为我国石油气体标准参比条件下的高位发热量和相对密度，则更宽的高位发热量范围为18.64~44.73MJm\*,相对密度范围为0.550~~0.900。天然气中其他主要组分摩尔分数的允许范围如下：CH4：
0.50αcH,1. 0
0≤zN,≤0. 50
0αc,H,0.20
0c,H,0. 05
管输气中微量和痕量组分含量范围见4.4.1。SGERG-88计算方法不能超出以上范围使用。附录B所描述的计算机执行程序不允许组成范围超过以上各极限值。
4.5不确定度
4.5.1管输气压缩因子计算的不确定度SGERG-88计算方法，在温度263～338K，天然气组成为zN,≤0.20、xco,≤0.09、αc,H。≤0.10、zH≤0.10、30MJ·m-3≤H.≤45MJ·m-2、0.55≤d≤0.80(见图1)时，计算管输气压缩因子，其计算结果的预期不确定度 △Z 如下：压力在最高为 10 MPa 的范围内时为士0.1%;压力在 10~~12 MPa 时为±0.2%。
当xco,>0.09时，在温度为263～338K的范围内，仅当最大压力为6MPa时，计算结果的不确定度△Z才能保持在土0.1%以内。不确定度水平是通过比较实测的天然气压缩因子数据而得到的。4.5.2更宽的应用范围压缩因子计算的不确定度超出4.5.1给出气质范围的气体压缩因子计算的预期不确定度见附录E。4.5.3输入变量不确定度的影响
表1列出的是相关输人变量的典型不确定度值，这些值可在最优操作条件下获得。根据误差传播分析，输人变量的不确定度会对压力为6 MPa，温度在263～~338 K范围内的压缩因子计算结果产生约土0.1%的附加不确定度。当压力大于6MPa时，附加不确定度会更大，且大致与压力成正比例增加。
表1相关输人变量的典型不确定度值输人变量
绝对压力
热力学温度
相对密度
高位发热量
4.5.4结果的表述
绝对不确定度
±0. 02 MPa
± 0. 15 K
±0. 06 MJ ·m-$
压缩因子计算结果应保留至小数点后四位，同时给出压力和温度以及所便用的计算方法(GB/T 17747.3,SGERG-88计算方法）。验证计算机程序时，压缩因子计算结果应给出更多的位数。377
bHo（0)
bHo（1)
bho(2)）
bhi（0)）
b(2)）
bHz（0)
bH2（1)
bH2（2)
b,（2)）
CHo(O))
CHo（1)
CHo（2)）
CHi(O)）
CHi(1)
CHi(2)）
CH2（O)）
CH2(1)
CH（2)）
GB/T 17747. 3-—1999
附录A
(标准的附录）
符号和单位
B,摩尔发热量（HcH)展开式中的零次项（常数)[方程(B20)B1i摩尔发热量(HcH)展开式中的-次项(次)[方程(B20)]B摩尔发热量（HcH)展开式中的二次项（平方)[方程（B20)]bHo温度展开式中的项［方程（B21)］bHi温度展开式中的项[方程（B21)]bH2温度展开式中的项［方程(B21)]bi,温度展开式中的项[方程(B22)］第二维利系数[方程(1)]
组分i和组分j间二元交互作用第二维利系数［方程（B22)］C111摩尔发热量(HcH)展开式中的零次项（常数)[方程(B29)]C1m摩尔发热量（HcH）展开式中的一次项（一次）[方程（B29)C1n摩尔发热量（HcH）展开式中的二次项（平方）[方程（B29)CHo温度展开式中的项[方程(B30)]CHi温度展开式中的项[方程（B30)]CH2温度展开式中的项［方程（B30)单位
m2·kmol-1
m'. kmol MJ-?
m2 kmol-1
m\.kmol-1.K-1
m2.kmol-1·K-2
m°·MJ-I
m3.MJ-1.K-1
m2.MJ-1.K-2
m2 . kmol .MJ-2
m*.kmol .MJ-2.K-1
m'. kmol ·MJ-2. K-?
m2.kmol-1
m2.kmol-1.K-1
m2.kmol-1 ·K-2
m2. kmol-1
m'.kmol-1
m'.kmol-2
m°.kmol-1.MJ-1
m6·MJ-2
m2.kmol-2
m*.kmol-2.K-1
m°* kmol-2.K-2
m°.kmol-1.MJ-1
m°.kmol-1.MJ-1.K-1
m°kmol-1.MJ-1·K-2
m°.MJ-2 .K-1
m6.MJ-2.K-2
Cun（0)
Cix(1)
Cijk（2)
附加的下标
GB/T17747.3—1999
Cii温度展开式中的项[方程（B31)第三维利系数[方程(1)］
组分i、组分j和组分k间三元交互作用第三维利系数[方程（B31)]相对密度[d(空气)一1,方程(B1)]选代计算中摩尔发热量HcH的变化值［方程(B10)和(B11)]高位发热量
摩尔发热量
摩尔质量［方程(B5）和（B8)
绝对压力
摩尔气体常数
热力学温度
摄氏温度=T—273.15，方程（B27)靡尔体积（=1/pm）
组分的靡尔分数
二元非同类交互作用维利系数B12和B1s（表B1)和三元非同类交互作用维利系数Ci的混合规则参数[方程（B32)]压缩因子
质量密度［方程(B8)和(B42)
摩尔密度(=1/Vm)
标准状态(T,=273.15K，p=101.325kPa)等价烃类
一氧化碳
二氧化碳
m°.kmol-2
m.kmol~2,K-1
m2.kmol-2.K-2
m6. kmol-2
m°.kmol-?
MJ ·kmol-1
MJ·m3
MJ · kmol1
kg·kmol-1
MJ · kmol-1. K-1
m2.kmol~1
kg·m-3
kmol ?m-3
附加的后缀
（空气）
（理想）
GB/T 17747.3--1999
标准组成的于空气方程（B1)
方程B(11)中使用的特别β值
等价烃［方程（B12)和（B15)
氮气［方程（B12)和（B16)
二氧化碳［方程（B12)和（B17)］氢气［方程（B12)和(B18)］
氧化碳［方程（B12和（B19)
理想气体状态
送代计数码（B2.1）
送代计数码（B2.2)
送代计数码（B4)
附录Bbzxz.net
(标准的附录）
SGERG-88计算方法描述
本附录给出了用于SGERG-88计算方法的方程和系数值。同时描述了SGERG-88计算方法所采用的计算机执行程序。该程序提供了标准的求解方法。验证计算机程序用的压缩因子数据见附录C。如果计算机程序能够得到与之相等（偏差在10-5之内)的计算结果，则可使用。计算结果应如附录C中示例保留至小数点后四位。B1
SGERG-88计算方法的计算机执行程序压缩因子Z的计算按4.2所述分3个步骤进行，如图B1所示。3N
GB/T 17747. 3-1999
输人数据
p.t.H..d,rco,+xH2
计算中间数据;T,一273.15K
P,,ICO+EcH(u),EN,(u),Hch(u)
Mch(u),p.(u),B.(u).Pa.a(v),H.(0)（见B2）
计算维利系数:T=(t+273. 15)K
B(T,Hch,I)),C(T,HcH.I)
（见B3）
解维利方程：
Z1+Bpm(T,p.a,)+Cp&(T.p.r)
(见 B4）
图B1SGERG-88计算方法流程图
（;i组分的摩尔分数）
B1.1输人数据，包括压力、温度、高位发热量、相对密度以及CO2和H2的摩尔分数。前三个参数值的单位凡不是MPa、K和MJ·m-3的，首先必须按附录D中给出的换算关系分别换算成以MPa、K和MI·m-\为单位的值。然后，用输人数据计算下列中间数据：烃类气体的摩尔分数
N2的魔尔分数
CO 的靡尔分数
等价烃的摩尔发热量
等价烃的摩尔质量
第二维利系数(T,一273.15K)
标准状态下的靡尔密度
标准状态下的质量密度
气体的高位发热量
注B1：方程(B1)(B46)中，每一个符号代表一个物理量除以所选单位（见附录A),因而每一个符号是一个无量纲的数值。
B1.2在所要求的温度下，用中间数据计算天然气第二维利系数和第三维利系数：B(T,HcH，x.)和C(T,HcH,r:)。
B1.3将B1.2求得的第二维利系数B和第三维利系数C代人维利方程，计算给定压力和温度下的压缩因子。
注B2：所用符号的定义见附录 A。B2中间数据的计算
用图B2中给出的选代方法，由方程(B1)～(B8)计算 8个中间数据（ccH、zNz、&co、HcH、McH、B,、pm,vp,）。这些方程中所使用的常数值见表B1。pn = dp(空气)
xco 0. 096 4rHz
（B1）
（B2)
GB/T 17747. 3—1999
Vmn（理想）= RT,/p元
Pm.,()=[Vm.n(理想）+ B,(u)]-1McH(u)=—2.709328+0.021062199HcH(u—1)输人数据：pt.H..d.rco,TH2
计算：Pxco
方程，(B1),(B2)
u=0,v=0
Hch(μ=0) =1000
B.(v= 0) = ~ 0. 065
计算:Pm.n(v=0)
方程：(B3),(B4)
计算：
ICH(u),rN, (u), McH(u),P,(u)方程(B5)～(B8)
Ip,p,(u)/10-6
方程(B9)
童成立
计算：T,=273.15K
Bch(u),BN(u),pm.s(v),H,(u)
方程(B12)～(B25)
不成立
H, H,(v)/<10
方程（B26）
计算结果;XcHIN,Ica.HcH
HcH(u) - Hch(u-1)+DHcH(u)
方程(B10)
计算,DHch(u)
方程(B11)
不成立
图B2中间数据选代计算的流程图（B3)
( B4 )
·（B5)
rch(u) - H./[Hch(u -- 1)pmn(v)] - [(αH,HH, + tcoHco)/Hech(u - 1)]...**( B6 )αn,（u）)= 1- αch(u)— aco, zh,·( B7)
pn(u) = Exch(u)Mch(u) + rn,(u)Mn,Jom.n() + (rco,Mco, + zh,MH, + coMco)pm.(v)中中心心
.( B8 )
GB/T17747.3--1999
B2.1用摩尔发热量HcH选代计算（内循环）按顺序从方程（B1）～（B8)进行计算，在第u次选代得到第一组近似值。选代计算初值是：HcH(u=0)-1 000 MJ kmol-1
B,(u=0)= -0. 065 m2 .kmol-1
方程(B1)～(B8)中所使用的其他常数值见表B1。表B1方程(B1)～(B8)所使用的常数值（同GB/T11062—1998)常
Vmn（理想）
o（空气）
0. 008 314 510
22. 414 097
MJ · kmol-1
MJ·kmol-1
kg·kmol-1
kg ·kmol-1
kg·kmol-1
kg·kmol-1
MJ · kmol-{K-1
m2. kmol-!
kg·m-$
内选代循环的收敛判断标准是标准状态下气体密度计算值p,(u)与标准状态下已知气体密度值p,（可直接测量，或由相对密度计算得到)之差的绝对值小于10-6,即：Ipn p(u)/ 10-
如果未满足，则用方程（B10)计算方程(B5）～(B8)中所使用的摩尔发热量HcH(u）的改进值：Hch(u) -- HcH(u - 1) + DHcH(u)其中：
DHch(u) [pn - p,(u)Jp(D) - pn(u)J-1式中：P,(u）-当前选代下的密度值[由HcH(u—1)开始计算：.........( B10 )
( B11 )
p(D)用[Hch(u—1)+1]作磨尔发热量输人数据，通过方程(B4)～(B8)求得的密度。当方程(B9)左边小于10-6时，本次送代计算结束，用第二维利系数的选代计算开始。B2.2用第二维利系数B,迭代计算（外循环）由前面迭代计算得到的中间数据 rcHu），αn,（u）,&co和Hch(u)以及输人数据 rco,和 H,计算整个气体在标准状态下第二维利系数B,(u)的改进值。天然气第二维利系数由方程(B12)求得：B(T) =B + 2iB12 + 2i,B1 + 2B + 2xixsB1s + B22 + 2xzBz3+2B2+B +B4 +Bss
注B3：方程(B12)中缺少的一些项，如 B25、Bgs等不会提高计算准确度，故设为零。B,(u) = B(T.)
式中：
TT,= 273.15K
i= rCH(u)
z n,(u)
= acoz
（B12)
（B13)
（B14）
（B15）
·B16)
·（B17）
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。