本标准规定了判断和处理Ⅰ型极值分布总体的随机样本中所出现的异常值的一般原则和实施方法。 GB 6380-1986 数据的统计处理和解释 I型极值分布样本异常值的判断和处理 GB6380-1986 标准下载解压密码：www.bzxz.net
本标准规定了判断和处理Ⅰ型极值分布总体的随机样本中所出现的异常值的一般原则和实施方法。

1引言
中华人民共和国国家标准
数据的统计处理和解释
I型极值分布样本异常值的判断和处理Statistical interpretation of data -Detection and handiing of outlyingobservations in the sample of type Iextreme yalue distribution
UDC 519.25
GB 6380 -86
1.1：本标准规定了判断和处理I型极值分布总体的随机样本中所出现的异常值的一般原则和实施方法。
I型极值分布也称贡贝尔（GumbeI）分布，其分布函数为F (r) =exp(-eu)
概率密度函数为
f(r)-exp(--e\\)
其中：y=（r-α）/b，b>0，
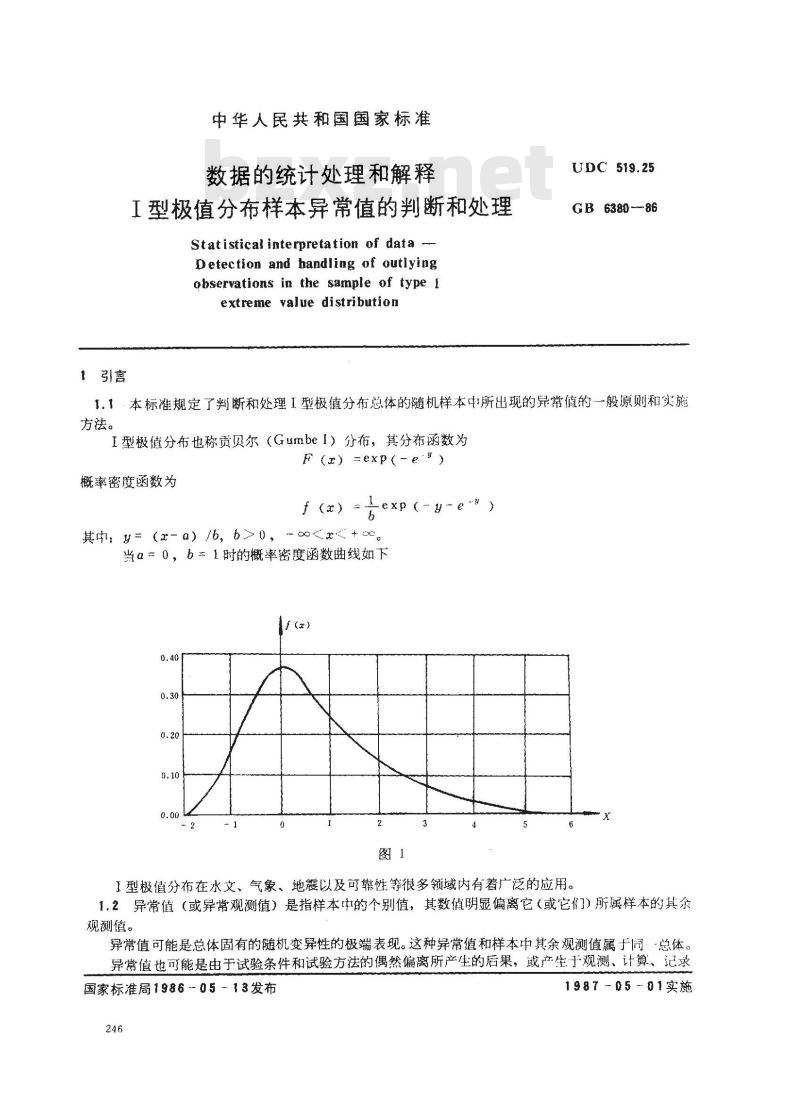
当α=0，b1时的概率密度函数曲线如下t (a)
1型极值分布在水文、气象、地震以及可靠性等很多领域内有着广泛的应用。1.2异常值（或异常观测值）是指样本中的个别值，其数值明显偏离它（或它们）所属样本的其余观测值。
异常值可能是总体固有的随机变异性的极端表现。这种异常值和样本中其余观测值属于同··总体。异常值也可能是由于试验条件和试验方法的偶然偏离所产生的后果，或产生于观测、计算、记录国家标准局1986-05-13发布
1987-05-01实施
GB 6380-86
的失误。这种异常值和样本中其余观测值不属子同一·总体。1.3本标准使用的其它统计学名词，见GB3358一82《统计学名词和符号》。1.4应用条件：当有充分理论根据或经验，确信所检验样本中诸观测值，除了个别异常值外，其余大部分值称为样本主体一来自同个「型极值分布总体。当样本主体自同·个I型极小值分布时，经过变换Z=一X后所得的样本主体可以认为是I型极值分布。
丁型极小值分布的分布函数为
F (α)=1- exp (-e)
其概率密度函数为
其中：=（α-a)/b，b0，
f(α）
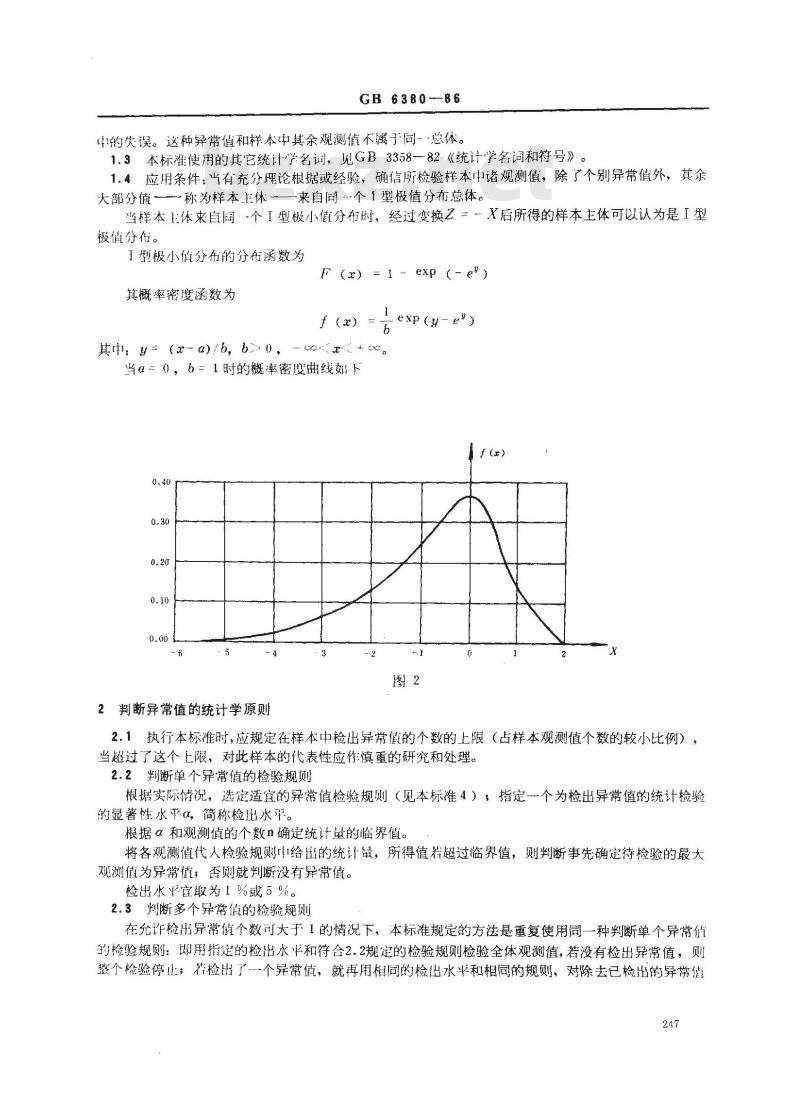
当α=0，b=1时的概率密度曲线下0.4h
2判断异常值的统计学原则
Texp(y-e\)
2.1执行本标准时，应规定在样本中检出异常值的个数的上限（占样本观测值个数的较小比例），当超过了这个上限，对此样本的代表性应作慎重的研究和处理。2.2半判断单个异常值的检验规则根据实际情况，选定适室的异常值检验规则（见本标准4），指定个为检出异常值的统计检验的显著性水平α，简称检出水平。根据α和观测值的个数n确定统计量的临界值。将各观测值代人检验规则给出的统计量，所得值岩超过临界值，则判断事先确定待检验的最大观测值为异常值，否则就判断没有异常值。检出水平宜取为1%或5%。
2.3判断多个异常值的检验规则
在允诈检出异常值个数可大于1的情况下，本标准规定的方法是重复使用同一种判断单个异常值的检验规则：即用指定的检出水平和符合2.2规定的检验规则检验全体观测值，若没有检出异常值，则整个检验停止；若检出了-个异常值，就再用相同的检出水半和相同的规则，对除去已检出的异常值247
GB 6380-86
后余下的观测值继续检验·…，直到没有检出异常值，或检出的异常值个数超过上限为止。3处理异常值的一般规则
3.1对用统计方法检出的异常值，应尽可能寻找产生异常值的技术上的，物理上的原因，作为处理异常值的依据。
3.2处理异常值的方式有：
异常值保留在样本中，并参加其后的数据分析；允许剔除异常值，即把异常值从样本中剔除，充允许剔除异常值，并追加适宜的观测值计入样本；在找到实际原因时修正异常值。3.3标准使用者应根据实际问题的性质，权衡寻找产生异常值原因的花费，正确判断异常值的得益及错误剔除正常观测俏的风险，确定实施下述三个规则中的一个：a、对任何异常值，若无充分说明其异常的技术上的、物理上的原因，则不得剔除或进行修正。b。异常值中除有充分说明其异常的技术上的、物理上的原因者可以剔除或进行修正外，如果在统计上表现为高度异常的，也允许剔除或进行修正。统计上表现为高度异常的意义是：指定一个为检验异常值是否高度异常的统计检验的显著性水平α*，简称剔除水半，其值小于检出水平α，实施时，按2.2规定进行检验后，再按2.2规定以剔除水半α*代替检出水平α，对检出的异常值进行检验，若在剔除水平α*下此检验是显著的，则此异常值表现为高度异常。在重复使用同一检验规则的情况下，每次检出了异常值后都要再检验它在剔除水平下是否高度异常，若某次检验中检出的异常值为高度异常，则这个异常值及在它前面检出的异常值都可被剔除或进行修正。
除特殊情况外，剔除水平一般宜取为1%，而不宜取大于5%的值。在选用剔除水平的情况下，检出水平可取5%或再稍大些。c。检出的异常值都可被剔除或进行修正。3.4被检出的异常值及剔除，修正的理由应予以记录，以备查询。4判断和处理异常值的规则
4.1本标准规定：当样本大小5n≤30时，使用狄克逊（Dixon）型检验法，当样本大小30n50时，使用欧文（Irwin）型检验法。4.2狄克逊型检验法——样本大小5≤n≤30情形4.2.1检验步骤
从样本观测值t挑选出最小观测值X（1），最大观测值X（），次大观测值X（n-1）以及第a.
大观测值X（α-2），计算统计量X (n)-X (r-1)
X(n)-X(t)
X(m) - X (n-2)
X (n)-X (1)
5≤n30
确延检出水半a，由附表1查出对应于n，α的临界值D,-。（n）。b.
当DD，（n）时，判断最大观测值X（n)为异常值，否则就不能判为异常值。c.
在给出剔除水α*的情况下，由附表1查出对应于n，α*的临界值D\a*（n），当DD*（n）时，判断X（n）为高度异常，否则就判断为没有高度异常的异常值。248
4.2.2示例
GB6380—86
启动剪床切断钢料，每口记录最初剪下的100根钢料的长例1（使用狄克逊型检验法的示例）度，作-批数据，-周内记录了6批，得到每日最大值数据如下：（单位：mm）321.46，319.62，320.44，319.51，329.73，320.41。现在检验其中最大值是否异常。根据经验，可以认为上述样本丰体来自同个1型极值分布，从这些观测数据中挑出最小值为X（1）一319.51，最大值为X(6）=329.73，次大值为X（5）=321.46，对n=6，计算统计量D=rio
(6)- X (5)—=329.73-321.46免费标准下载网bzxz
X(6)-X(1)
329.73-319.51
取检出水平α=5%，查附表1得D的临界值Do.95（6）=0.681,由于D=0.809-0.681-D.g（6），故判断X（6）-329.73为异常值。又取剔除水平α*=1%，套附表1得Do.g（6）=0.796,山1D：Do.s（6），故判断X（(）=329.73为高度异常。经复核查实，此数据系误记，实际值为319.73。例2（重复使用狄克逊型检验法以判断多个异常值的示例）从某种绝缘材料中随机地取出11个样品，在定条件下进行寿命试验，其失效时问分别为（单位：h）4.09,17.31, 60.78,62.16,64.15,70.67,71.85,75.50,79.35,80.00, 88.01。现在检验4.09，17.31是否异常。理论工表明这种绝缘材料的寿命T服从I型极小值分布，因此经变换X一T后所得的样本可以认为是1型极值分布的，即对来【型极值分布的样本X（1）=一88.01，X。2）一·80.00，=62.16，X(）=-60.78，X（10)=-17.31，X（）=4.09，检验最大观测值X（m）及次X（B）=
大观测值X（10)是否异常。这里n=11，计算统计量D= r2n =
X(n) - X()
X(10) - X(1)
(-4.09) - (- 60.78)
(- 4.09) - (~- 88.01)
取检出水平α=5%，查附表1得D的临界值Do.9s（11）=0.656，由于DDu.95（11），故判断X(11）=4.09为异常值。再对余下的10个数据继续检验，仍取检出水乎α=5，对n=10，计算统计量
X(10)-X(+) = (-17.31)-(-62.16)= 0.634D= r20=X.m)-X(1)
(- 17.31)-(- 88.01)
查附表1得)的临界值Do.95（10）=0.676，出于/）：Dm.95（10），故不能认为X(w）=－17.31为异常值。
4.3欧文型检验法
样本大小30°m%50情形
4.3.1检验步骤
从样本观测值中挑选出最小观测值X（1），最大观测值X（n)，以及次大观测值X（1），a.
计算统计量
X (n)-
E(Xi)-Xn)2
GB6380—86
这里求和是对除去最小观测值X（1)以及最大观测值X（\)后的所有样本观测值进行的。b．确定检出水α，由附表2查出对应于n,α的临界值「-α（n）。当I1i-α(n)时,判断最大观测值X(n)为异常值，否则就不能判为异常值。C
d．在给出剔除水平α*的情况下，由附表2查出对应于n，α*的临界值1-a（n）。当I11-a（n）时，判断X（n)为高度异常，否则就判断为没有高度异常的异常值。4.3.2系例
例3（使用欧文型检验法的示例）某地某河流年最大经流量的逐年观测数据如下：（单位：km3/s)
1.69, 1.22, 0.75, 1.26, 1.73, 1.74, 3.09, 1.57, 1.97, 2.23, 2.03, 1.58, 0.90, 2.40, 1.65,1.96,2.30,1.79,1.48,2.22,1.91,3.06,2.08,1.06,4.31,1.56,1.88,2.10,2.02,1.74,1.18,2.12,1.38,0.90,1.45,1.78,1.97,2.27，2.34，2.44。现在检验最大值X（40）=4.31是否异常。可以认为年最大经流量的逐年观测数据近似地服从1型极值分布。对上述观测数据稍加整理可以看出，其最小值X（1）=0.75，最大值X（40）=4.31以及次大值X（39，=3.09，对除去X（1)和Xah）后的所有数据，先计算S=0.502，再算得统计量「的值I=In
Xe40)X(39）
4.31-3.09
取检出水平α=5%，查附表2得I的临界值0.95（40）=2.84，由于『1a.95（40），故不能认为X（40）=4.31是异常值。
X(n)- X(a-1)
X(n)-Xa)
X(n)-X n-2)
X(n)-X u)
GB 6380-86
附录A
（补充件）
狄克逊型检验法的临界值表
GB6380-86
欧文型检验法的临界值表
注：本表是在DPS8-45计算机上统计模拟M=10000次的结果。附加说明：
本标准由全国统计方法应用标准化技术委员会提出。本标准由全国统计方法应用标准化技术委员会数据的处理和解释分委员会工作组起靠。本标准主要起草人马逢时、许其洲、史道济。232
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。