GB 4090-1983
基本信息
标准号: GB 4090-1983
中文名称:数据的统计处理和解释 泊松分布参数的检验
标准类别:国家标准(GB)
英文名称:Statistical interpretation of data--Test for parameter in Poisson distribution
标准状态:已作废
发布日期:1983-12-21
实施日期:1984-10-01
作废日期:2009-01-01
出版语种:简体中文
下载格式:.rar.pdf
下载大小:203160

标准分类号
标准ICS号:数学、自然科学>>07.020数学
中标分类号:综合>>基础学科>>A41数学
关联标准
替代情况:被GB/T 4089-2008代替
出版信息
出版社:中国标准出版社
页数:9页
标准价格:8.0 元
出版日期:1984-10-01
相关单位信息
首发日期:1983-12-21
复审日期:2004-10-14
起草人:孙山泽、高惠漩
起草单位:全国统计方法应用标准化技术委员会数据的处理和解释分委员会工作组
提出单位:全国统计方法应用标准化技术委员会
发布部门:国家标准局
主管部门:国家标准化管理委员会
标准简介
本标准所用统计学名词见国标GB 3358-82《统计学名词及符号》。 GB 4090-1983 数据的统计处理和解释 泊松分布参数的检验 GB4090-1983 标准下载解压密码:www.bzxz.net
本标准所用统计学名词见国标GB 3358-82《统计学名词及符号》。
本标准所用统计学名词见国标GB 3358-82《统计学名词及符号》。
标准图片预览




标准内容
1引言
中华人民共和国国家标准
数据的统计处理和解释
泊松分布参数的检验
Statstical interpretation of dataTest for parameter in Poisson distribution1.1本标准所用统计学名词见国标GB3358—82《统计学名词及符号》。1.2本标准所讨论的总体为泊松分布X=xlal
x=0,1,2,
UDC 519.25
GB 4090--83
式中≥0为分布参数。本标准基于独立随机样本xI,x2,x,规定了检验与参数有关给定假设的方法。当有充分的理由确信总体服从泊松分布时,可以采用本标准。1.3用H。表示原假设,H,表示备择假设。入。>0是给定值。本标准讨论三种情况:Hot A = o,
Ho: aHo: aao,
Hi: a。
H:>。
Hi: a选用哪一种类型的检验,根据具体问题的需要而定。2双侧检验Ho: = α。
2.1实施步骤
(双侧检验)
(单侧检验)
a。由αo,样本大小n及给定检验的显著性水平a,确定拒绝域的临界值Ci,Cz。(c1,C2的确定见2.2),
b。计算T=三x,的值;
,当T,或≥时,拒绝Ho,当,c,c,可由。,n及α确定,c,是满足下式的最大整数:E(na。)
TC2是满足下式的最小整数
p? T2c2ndo!
(nao)k
一用A
相应的第一类错误的概率和第二类错误的概率见附录A(补充件)。可以用×?分布表法或正态近似法确定 1、z
2.2.1×2分布表法
Ci是满足下式的最大整数
国家标准局1983-12-21发布
C2是满足下式的最小整数
1984-10 01实施
GB 4090-83
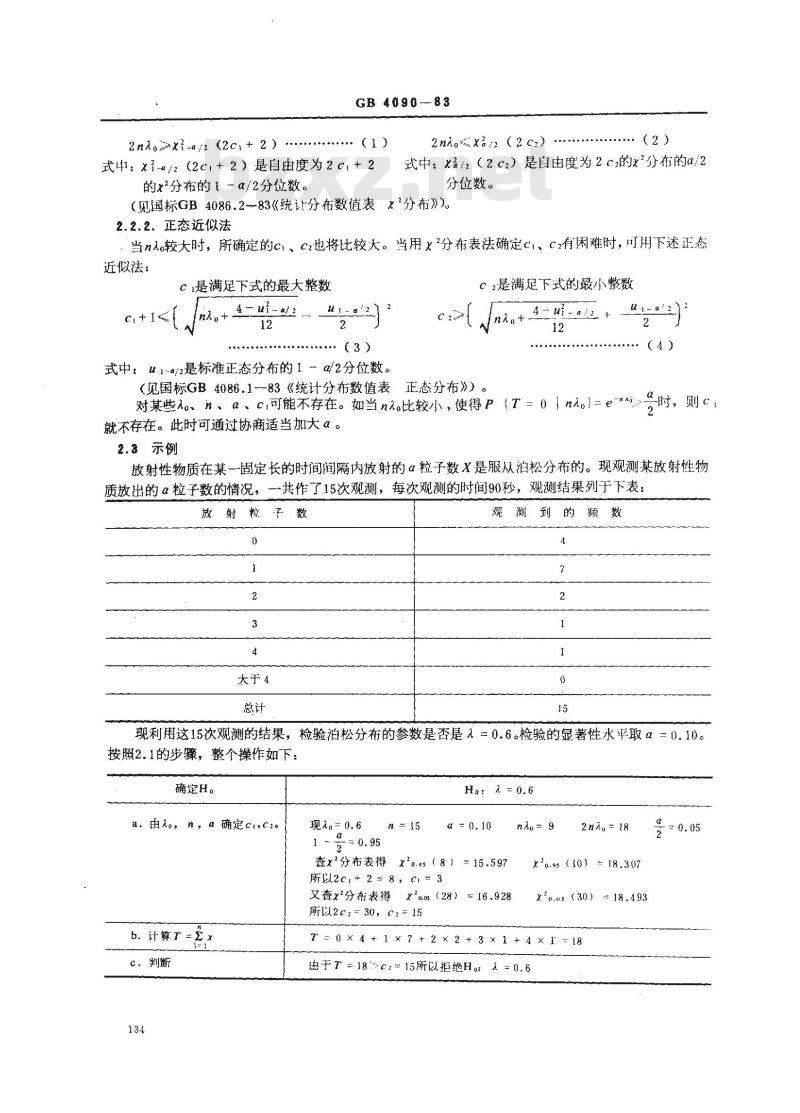
2nl.x+-+/2 (2c++ 2)***.+****+* (1)式4:×-/2(2c+2)是由度2c+2的x2分布的1-α/2分位数。
2noxa/2 (2c2)
式中:2(2c2)是自由度为2c的2分布的a/2分位数。
(见国标GB4086.2--83《统计分布数值表×分布》)2.2.2、正态近似法
当n1较大时,所确定的c1、C2也将比较大。当用×分布表法确定ci、C2有闲难时,可用下述正态近似法:
C1是满足下式的最大整数
4-ui-a/2
式中:u1-a/2是标准正态分布的1-α/2分位数。C2是满足下式的最小整数
4 - ui-a/2
ui-al2
(4)
(见国标GB4086.1--83《统计分布数值表正态分布》)。~时,则℃
对某些o、n、α、i可能不存在。如当no比较小,使得(=ne-\就不存在。此时可通过协商适当加大α。2.3示例
放射性物质在某一固定长的时间间隔内放射的α粒子数X是服从泪松分布的。现观测某放射性物质放出的α粒子数的情况,一共作了15次观测,每次观测的时间90秒,观测结果列于下表:放射粒子数
太于4
观测到的频数
现利用这15次观测的结果,检验泊松分布的参数是否是入=0.6。检验的显著性水平取α=0.10。按照2.1的步骤,整个操作如下:确定H。
a、由a,n,a 确定ct,cia
b、计算
c.判断
现。=0.6
n = 15
Ha: 元=0.6
α = 0.10
查分布表得
×0.95(8)
所以2c,+ 2=8,i= 3
又查x\分布表得x00s(28)
所以2c2= 30,C,=15
=0×4+1×7
nho= 9
2nag= 18
x*0.95 (10) - 18.307
x*0.05 (30)- 18.493
由于=18>℃2=15所以拒绝Ho:=0.6=18
3单侧检验Ho:^oWww.bzxZ.net
3.1实施步骤
GB4090-83
a.由u,样本大小n及给定的检验的显著水平α,确定拒绝域的临界值℃,(c2的确定见3.2)。b.计算T=≥,x,的值。
c.当Tc时,拒绝Ha,当T时,不拒绝Ho3.2:拒绝域临界值c2的确定
c,可由入。,n及a确定。它是满足下式的最小整数:Tic2 / nad) -Z-(ndo)
相应第-·类错误的概率和第,二类错误的概率见附录A(补充件)。可以用x‘分布表法或正态近似法确定C2。
3.2.1x分布表法
C2是满足下式的最小整数:
2n/0x? (2c2)
式:(2c2)是自由度2c的×分布的a分位数。3.2.2正态近似法
C2是满足下式的最小整数:
式中:ul-a是标准正态分布的1—α分位数。2
如同双侧检验一样,当利用分布表法有困难时,可使用正态近似法。4单侧检验Ho:1
4.1实施步骤
(5)
(6)
由。,样本大小n及给定的检验的显著性水平α,确定拒绝域的临界值c;(c,的确定见4.2)。a.
b.计算T=艺xi的值。
c.当Tc,时,拒绝Ha,当Tci时,不拒绝Ho4.2拒绝域临界值c,的确定
Ct由,n及α确定,它是满足下式的最大整数。=(ndo)
相应第一类错误的概率和第二类错误的概率见附录A(补充件)。可以用‘分布表法或正态近似法确定ci。
4.2.1×2分布表法
C,是满足下式的最大整数:
2nAoxi-a (2ci+ 2)
式中:×-α(2cl+2)是2c,+2自由度×分布的1-α分位数。4.2.2正态近似法
Ci是满足下式的最大整数:
式中:u-是标准正态分布的1
GB 4090—83
a分位数。
当利用x分布表法有困难时,可使用正态近似法。136
GB 4090—83
附录A
两类错误
(补充件)
A.1第一类错误
第一-类错误的概率是当原假设为真时,拒绝原假设的概率。它可以表为拒绝域的临界值的函数。记作a。
Ho: =情形:α'=P (≤c ln) + (Tlna)= (T≤c-Ina) + 1-P (T≤cz- 1 /nao)Ho:o情形:a' (Tc2lndo) = 1(Cz1lnao)(当<时,总有())
Ho:情形:α'(c|n)
(当<时,总有(cn)α')
由于泊松分布的离散性,拒绝域的临界值是整数,α常常不是正好等于给定的显著性水平α,而是比α小。
A.2第类错误
第:类错误的概率是原假设错误时,没有拒绝原假设的概率,它可以表示为拒绝域的临界值和所考虑的备择假设中特定的入值的函数,记作β。Ha:o情形:β\= p (ci<Haa>情形:β=PT≥c,Ina,)=1P (T≤c,In)β'表示真实的第二类错误的概率,这个记号的使用仿效第一类错误的情况,检验的功效(即原假设不成立时,拒绝它的概率)为1-β\。A.3第一类错误的概率α'和第二类错误的概率β'的计算在给定H。、α、n的情况下,确定了拒绝域的临界值ciC2,可进--步计算:a实际的第一类错误的概率α是多大?b.对应于特别指定的备择假设Hi:α=a,第二二类错误的概率β'是多大?c.指定第二类错误的概率为β,其对应的入,值是多大?表A.1给出了计算α'和β'的几种方法。问题c.的解决见表A2
表A1中的正态近似方法,只适用于c,℃2较大时(大于15)。对Ho:=1情形,如果c2较大,而c,较小,在计算α或β'时,可对P(T考虑标准中2.3的示例:
原假设Ho:元=α。=0.6,n=15,显著性水平α=0.10,确定出的拒绝域的临界值c1=3,2=15。15个子样的总和T=
,x二18,进一步计算:
实际的第一类错误的概率α'是多少?a.
对特定的备择假设^=11=1.0,第二类错误的概率β是多大?b.
GB4090—83
对确定的β=0.1,对应的1,值是多少?本例nAo=9,nA,=15,Ci
A.4.1用泊松分布表
3,Cz=15,根据表A1可计算a',β39*
e-9+ 1
Z。k!
e 9- 0.0212 + 1 - 0.9585 = 0.06278=2e5-215
e+5=0. 4657 - 0. 0002 = 0.4655Po k!e
A.4.2利用x分布表
a=P (×2(2c/+ 2)≥2nAo)+ 1-P(×2 (2c2)2n/。=P×28)≥18)+1-P×2(30)181
= 0.0212 + 1 - 0.9585
β'= P( x2 (2cz) ≥2na1) - pA.4.3用正态近似
因c1=3,不宜用正态近似,而c2=15较大可用正态近似,故取pl Tα (×(2c+ 2)≥2n +1-Φ
= Px2 (8)≥18 + 1 - @ (1.72)= 0.0212 + 1 0.9573
3Vc,-V12na-3c2
=@(-0.09)-P(×2(8)30)
=0.4641-0.0002
P×2(2c+2)2na.
对给定的=0.1,求对应的特定备择假设入,的值,根据表A2进行。对双侧检验,对应β=0.1有两个值(),()
30%(30)
F-p(2c2)=
2n x (2c1+2)=
30x0.10(8)=
4090--83
(P2) +
()()
( a-0)0 1-0(08--27a ) =0
(38-at*- (07e )0 -(1
(08-1178)
(12)的的的心
08 a7-97e )o- 1= p(
(8a-e )o- 1+(1-i-1e)
(-a )0- 0e
(02) --
1yu(+132) 2x1
.......
10ru2(+102) 4x) d=,\
(El) yu-
(11) d-=
(yuI I+hel) d =g
(0u1151) d=,p
(81) 66666多+++?
('y2k (352) -x)
109u2(332)x) d - 1 =,0
kll) -. oym-a-
x(oru)
(rul1-11) d=+g
(\yu z31) d =,n
1021 *>y 0H
( (+1) 2x) d - (\ ()
1yu< (32) 4x) d - 1+(0yu2(2+*2) tx) d=+Da
(ul>) d- (u-) d=-8
(u(-151) d-
I+(ayu I's) d =
(0u13) d+ (u/>1)
零假设和拒
绝域形式
利用分
布的计算
GB 4090--83
H。: α=Ao,T在此情形在入的两侧分别有
()和()
其对应的第二类错误概率为,它们的计算公式如下:
其中-(2c2)表示自由度为2c2的x分布的1 - β分位数。
-xe (2c++2) .. (28)
其中(2c+2)表示自由度为2c
+2的×分布的分位数。
表中计算和入附,因一般n和n
与na。相差很大,故忽略了p(cinai)和p(r>cIna\)
Hor lo,Tc?
+ (29)
xi-(2C2)表木自由
度为2c2的×分布的1
8分位数。
Hot A ho, T..r.
-x(2c,+2)
....... (30)
(2c+2)表示自由
度为2c,2的x2分布的β
分位数。
GB4090-83
附录B
种等效的检验方法
(参考件)
进行泊松分布参数入有关的检验,也可采用一种等效的方法:计算值T=
芝x。由T求出泊松分布参数的置信水平(1-α)的置信区间(置信区间的确定见国标GB4089--83《泊松分布参数的估计》)。在H:=情形,求双侧置信区间(,)在Ha:情形,求单侧置信区间(a,α),在Ho:情形,求单侧置信区间(0,)。当入的值在置信区间内时,不拒绝Ho,当入的值不在置信区间内时,拒绝Ho。附加说明:
本标准由全国统计方法应用标准化技术委员会提出。本标准由全国统计方法应用标准化技术委员会数据的处理和解释分委员会工作组起草。本标准主要起草人孙山泽、高惠璇。141
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。
中华人民共和国国家标准
数据的统计处理和解释
泊松分布参数的检验
Statstical interpretation of dataTest for parameter in Poisson distribution1.1本标准所用统计学名词见国标GB3358—82《统计学名词及符号》。1.2本标准所讨论的总体为泊松分布X=xlal
x=0,1,2,
UDC 519.25
GB 4090--83
式中≥0为分布参数。本标准基于独立随机样本xI,x2,x,规定了检验与参数有关给定假设的方法。当有充分的理由确信总体服从泊松分布时,可以采用本标准。1.3用H。表示原假设,H,表示备择假设。入。>0是给定值。本标准讨论三种情况:Hot A = o,
Ho: a
Hi: a。
H:>。
Hi: a
2.1实施步骤
(双侧检验)
(单侧检验)
a。由αo,样本大小n及给定检验的显著性水平a,确定拒绝域的临界值Ci,Cz。(c1,C2的确定见2.2),
b。计算T=三x,的值;
,当T,或≥时,拒绝Ho,当,
T
p? T2c2ndo!
(nao)k
一用A
相应的第一类错误的概率和第二类错误的概率见附录A(补充件)。可以用×?分布表法或正态近似法确定 1、z
2.2.1×2分布表法
Ci是满足下式的最大整数
国家标准局1983-12-21发布
C2是满足下式的最小整数
1984-10 01实施
GB 4090-83
2nl.x+-+/2 (2c++ 2)***.+****+* (1)式4:×-/2(2c+2)是由度2c+2的x2分布的1-α/2分位数。
2noxa/2 (2c2)
式中:2(2c2)是自由度为2c的2分布的a/2分位数。
(见国标GB4086.2--83《统计分布数值表×分布》)2.2.2、正态近似法
当n1较大时,所确定的c1、C2也将比较大。当用×分布表法确定ci、C2有闲难时,可用下述正态近似法:
C1是满足下式的最大整数
4-ui-a/2
式中:u1-a/2是标准正态分布的1-α/2分位数。C2是满足下式的最小整数
4 - ui-a/2
ui-al2
(4)
(见国标GB4086.1--83《统计分布数值表正态分布》)。~时,则℃
对某些o、n、α、i可能不存在。如当no比较小,使得(=ne-\就不存在。此时可通过协商适当加大α。2.3示例
放射性物质在某一固定长的时间间隔内放射的α粒子数X是服从泪松分布的。现观测某放射性物质放出的α粒子数的情况,一共作了15次观测,每次观测的时间90秒,观测结果列于下表:放射粒子数
太于4
观测到的频数
现利用这15次观测的结果,检验泊松分布的参数是否是入=0.6。检验的显著性水平取α=0.10。按照2.1的步骤,整个操作如下:确定H。
a、由a,n,a 确定ct,cia
b、计算
c.判断
现。=0.6
n = 15
Ha: 元=0.6
α = 0.10
查分布表得
×0.95(8)
所以2c,+ 2=8,i= 3
又查x\分布表得x00s(28)
所以2c2= 30,C,=15
=0×4+1×7
nho= 9
2nag= 18
x*0.95 (10) - 18.307
x*0.05 (30)- 18.493
由于=18>℃2=15所以拒绝Ho:=0.6=18
3单侧检验Ho:^oWww.bzxZ.net
3.1实施步骤
GB4090-83
a.由u,样本大小n及给定的检验的显著水平α,确定拒绝域的临界值℃,(c2的确定见3.2)。b.计算T=≥,x,的值。
c.当Tc时,拒绝Ha,当T时,不拒绝Ho3.2:拒绝域临界值c2的确定
c,可由入。,n及a确定。它是满足下式的最小整数:Tic2 / nad) -Z-(ndo)
相应第-·类错误的概率和第,二类错误的概率见附录A(补充件)。可以用x‘分布表法或正态近似法确定C2。
3.2.1x分布表法
C2是满足下式的最小整数:
2n/0x? (2c2)
式:(2c2)是自由度2c的×分布的a分位数。3.2.2正态近似法
C2是满足下式的最小整数:
式中:ul-a是标准正态分布的1—α分位数。2
如同双侧检验一样,当利用分布表法有困难时,可使用正态近似法。4单侧检验Ho:1
4.1实施步骤
(5)
(6)
由。,样本大小n及给定的检验的显著性水平α,确定拒绝域的临界值c;(c,的确定见4.2)。a.
b.计算T=艺xi的值。
c.当Tc,时,拒绝Ha,当Tci时,不拒绝Ho4.2拒绝域临界值c,的确定
Ct由,n及α确定,它是满足下式的最大整数。=(ndo)
相应第一类错误的概率和第二类错误的概率见附录A(补充件)。可以用‘分布表法或正态近似法确定ci。
4.2.1×2分布表法
C,是满足下式的最大整数:
2nAoxi-a (2ci+ 2)
式中:×-α(2cl+2)是2c,+2自由度×分布的1-α分位数。4.2.2正态近似法
Ci是满足下式的最大整数:
式中:u-是标准正态分布的1
GB 4090—83
a分位数。
当利用x分布表法有困难时,可使用正态近似法。136
GB 4090—83
附录A
两类错误
(补充件)
A.1第一类错误
第一-类错误的概率是当原假设为真时,拒绝原假设的概率。它可以表为拒绝域的临界值的函数。记作a。
Ho: =情形:α'=P (≤c ln) + (Tlna)= (T≤c-Ina) + 1-P (T≤cz- 1 /nao)Ho:o情形:a' (Tc2lndo) = 1(Cz1lnao)(当<时,总有())
Ho:情形:α'(c|n)
(当<时,总有(cn)α')
由于泊松分布的离散性,拒绝域的临界值是整数,α常常不是正好等于给定的显著性水平α,而是比α小。
A.2第类错误
第:类错误的概率是原假设错误时,没有拒绝原假设的概率,它可以表示为拒绝域的临界值和所考虑的备择假设中特定的入值的函数,记作β。Ha:o情形:β\= p (ci<
表A1中的正态近似方法,只适用于c,℃2较大时(大于15)。对Ho:=1情形,如果c2较大,而c,较小,在计算α或β'时,可对P(T
原假设Ho:元=α。=0.6,n=15,显著性水平α=0.10,确定出的拒绝域的临界值c1=3,2=15。15个子样的总和T=
,x二18,进一步计算:
实际的第一类错误的概率α'是多少?a.
对特定的备择假设^=11=1.0,第二类错误的概率β是多大?b.
GB4090—83
对确定的β=0.1,对应的1,值是多少?本例nAo=9,nA,=15,Ci
A.4.1用泊松分布表
3,Cz=15,根据表A1可计算a',β39*
e-9+ 1
Z。k!
e 9- 0.0212 + 1 - 0.9585 = 0.06278=2e5-215
e+5=0. 4657 - 0. 0002 = 0.4655Po k!e
A.4.2利用x分布表
a=P (×2(2c/+ 2)≥2nAo)+ 1-P(×2 (2c2)2n/。=P×28)≥18)+1-P×2(30)181
= 0.0212 + 1 - 0.9585
β'= P( x2 (2cz) ≥2na1) - p
因c1=3,不宜用正态近似,而c2=15较大可用正态近似,故取pl T
= Px2 (8)≥18 + 1 - @ (1.72)= 0.0212 + 1 0.9573
3Vc,-V12na-3c2
=@(-0.09)-P(×2(8)30)
=0.4641-0.0002
P×2(2c+2)2na.
对给定的=0.1,求对应的特定备择假设入,的值,根据表A2进行。对双侧检验,对应β=0.1有两个值(),()
30%(30)
F-p(2c2)=
2n x (2c1+2)=
30x0.10(8)=
4090--83
(P2) +
()()
( a-0)0 1-0(08--27a ) =0
(38-at*- (07e )0 -(1
(08-1178)
(12)的的的心
08 a7-97e )o- 1= p(
(8a-e )o- 1+(1-i-1e)
(-a )0- 0e
(02) --
1yu(+132) 2x1
.......
10ru2(+102) 4x) d=,\
(El) yu-
(11) d-=
(yuI I+hel) d =g
(0u1151) d=,p
(81) 66666多+++?
('y2k (352) -x)
109u2(332)x) d - 1 =,0
kll) -. oym-a-
x(oru)
(rul1-11) d=+g
(\yu z31) d =,n
1021 *>y 0H
( (+1) 2x) d - (\ ()
1yu< (32) 4x) d - 1+(0yu2(2+*2) tx) d=+Da
(ul>) d- (u-) d=-8
(u(-151) d-
I+(ayu I's) d =
(0u13) d+ (u/>1)
零假设和拒
绝域形式
利用分
布的计算
GB 4090--83
H。: α=Ao,T
()和()
其对应的第二类错误概率为,它们的计算公式如下:
其中-(2c2)表示自由度为2c2的x分布的1 - β分位数。
-xe (2c++2) .. (28)
其中(2c+2)表示自由度为2c
+2的×分布的分位数。
表中计算和入附,因一般n和n
与na。相差很大,故忽略了p(cinai)和p(r>cIna\)
Hor lo,Tc?
+ (29)
xi-(2C2)表木自由
度为2c2的×分布的1
8分位数。
Hot A ho, T..r.
-x(2c,+2)
....... (30)
(2c+2)表示自由
度为2c,2的x2分布的β
分位数。
GB4090-83
附录B
种等效的检验方法
(参考件)
进行泊松分布参数入有关的检验,也可采用一种等效的方法:计算值T=
芝x。由T求出泊松分布参数的置信水平(1-α)的置信区间(置信区间的确定见国标GB4089--83《泊松分布参数的估计》)。在H:=情形,求双侧置信区间(,)在Ha:情形,求单侧置信区间(a,α),在Ho:情形,求单侧置信区间(0,)。当入的值在置信区间内时,不拒绝Ho,当入的值不在置信区间内时,拒绝Ho。附加说明:
本标准由全国统计方法应用标准化技术委员会提出。本标准由全国统计方法应用标准化技术委员会数据的处理和解释分委员会工作组起草。本标准主要起草人孙山泽、高惠璇。141
小提示:此标准内容仅展示完整标准里的部分截取内容,若需要完整标准请到上方自行免费下载完整标准文档。